Adunarea și scăderea fracțiilor zecimale cu număr finit de zecimale

Regula de adunare: se trec fracțiile una sub alta, virgula să fie sub virgulă. Se face adunarea ca la numere naturale, iar la rezultatul final virgula se trece sub celelalte două virgule.

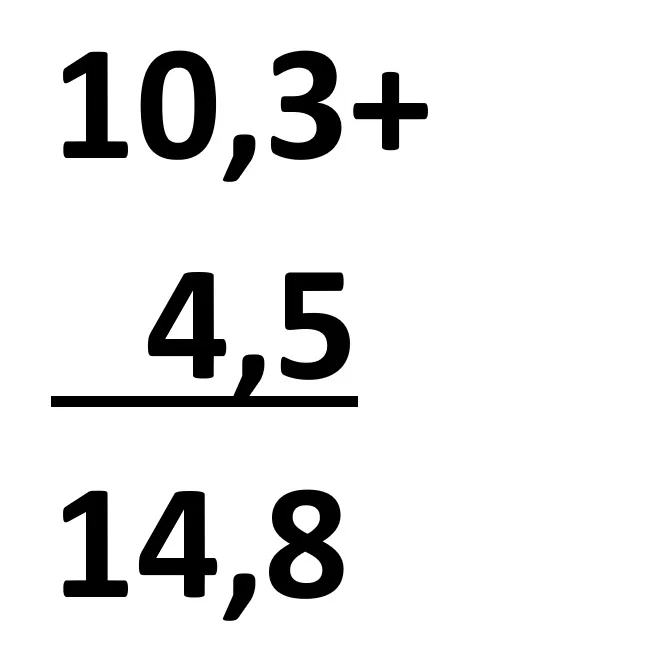
Dacă termenii nu au același număr de zecimale, adaugăm zerouri după ultima zecimală la numărul cu mai puține zecimale, pentru a avea același număr de zecimale.

Exemplu: 3,6 – 2,18 = 3,60 – 2,18 = 1,42

Pentru scădere se folosesc aceleași reguli.

Înmulțirea unei fracții zecimale cu număr finit de zecimale cu 10, 100, 1000, etc.

Înmulțirea unei fracții zecimale cu număr finit de zecimale cu un număr natural putere a lui 10 se face mutând virgula de la stânga la dreapta peste atâtea cifre cât este și exponentul puterii lui 10.

2,354  100 = 235,4. (100=102, am mutat virgula două cifre mai la dreapta)
0,075  1000 = 75;

Împărțirea unei fracții zecimale cu număr finit de zecimale la 10, 100, 1000, etc.

Împărțirea unei fracții zecimale cu număr finit de zecimale la un număr natural putere a lui 10 se face mutând virgula de la dreapta la stânga peste atâtea cifre cât este și exponentul puterii lui 10.

235,4 : 100 = 2,354. (100=102, am mutat virgula două cifre mai la stânga)
75 : 1000 = 0,075.

Înmulțirea unei fracții zecimale cu număr finit de zecimale cu un număr natural sau cu o altă fracție zecimală cu număr finit de zecimale

Regula este următoarea:

Se înmulțesc numerele fără a se ține cont de virgulă, apoi, la rezultat, se trece virgula numărând, de la dreapta la stânga, atâtea cifre câte zecimale au împreună cele două numere înmulțite.

Exemple:

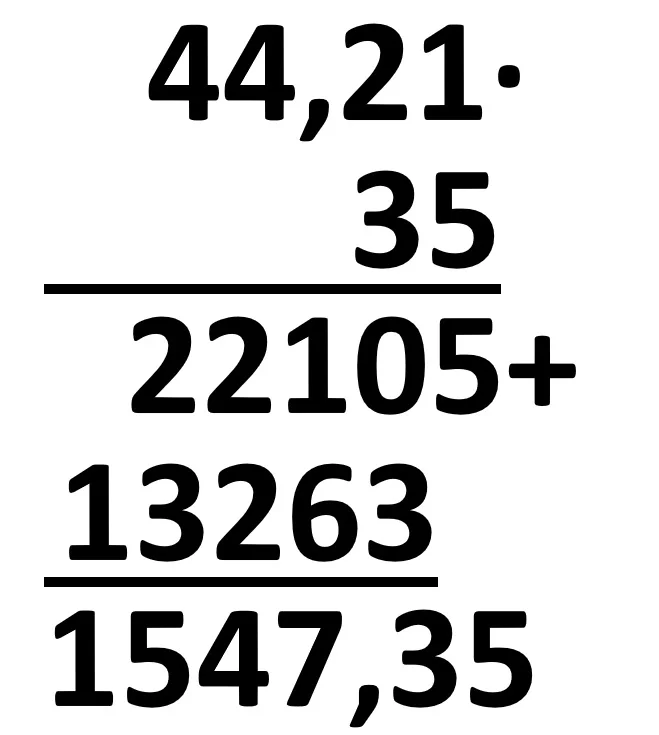
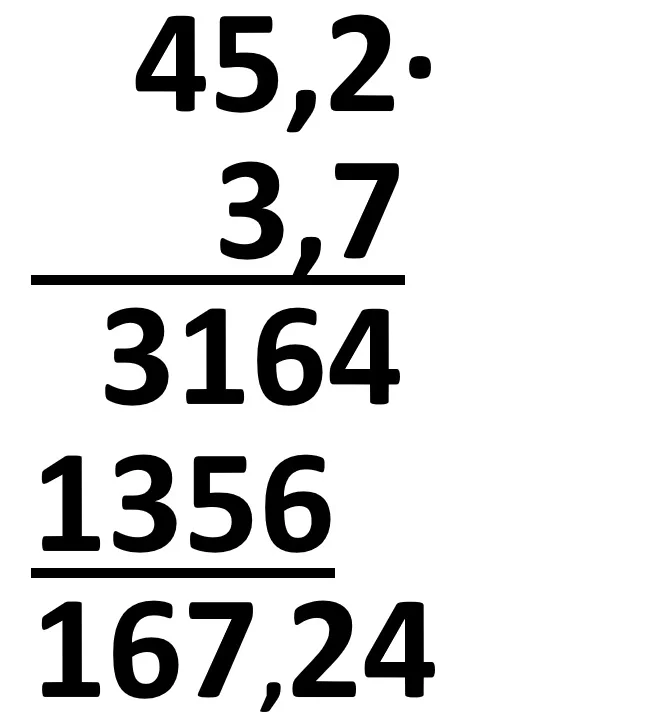
Împărțirea a două numere naturale cu rezultat fracție zecimală

Regula este următoarea:

Se împarte mai întâi partea întreagă la numărul dat, iar dacă împărțirea nu este exactă, se adaugă un 0 la rest și se scrie virgula la rezultat, apoi se continuă împărțirea, punând, de fiecare dată cifra 0 la noul rest. Prin împărțirea a două numere naturale se pot obține fracții zecimale finite (cu un număr finit de zecimale) sau periodice (cu număr infinit de zecimale).

Exemple:

Fracții zecimale finite

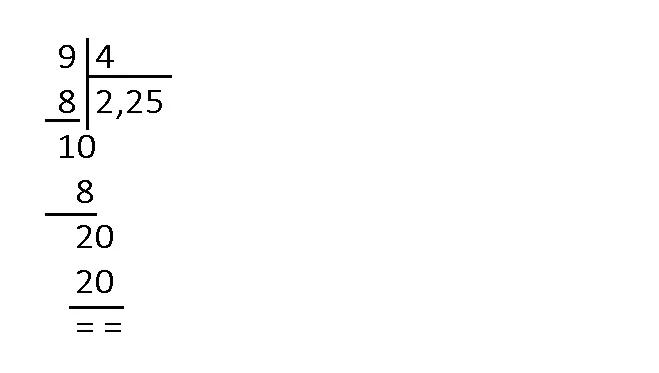
Rezultatul împărțirii 9 : 4 este 2,25.

Fracții zecimale periodice simple

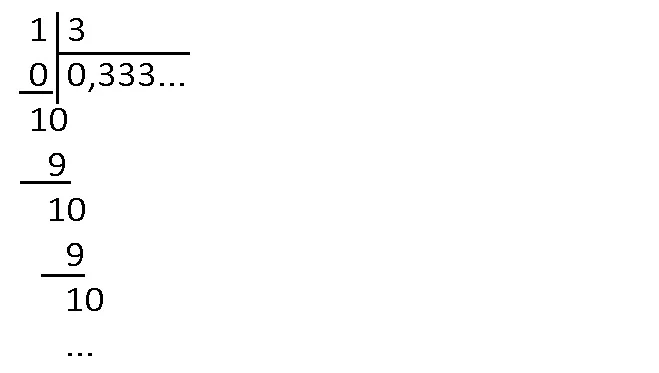
1:3 = 0,3333…

Observăm că zecimala 3 se repetă la infinit: spunem că 3 este o zecimală periodică, iar, la rezultat, îl vom trece în perioadă: 1:3 = 0,(3).

Observăm că grupul de cifre 740 se repetă la infinit, așadar, la rezultat, îl vom trece în perioadă: 47:27 = 1,(740).

Fracții zecimale periodice mixte:

Observăm că cifra 3 se repetă la infinit, deci scriem că 35:6 = 5,8(3).

Împărțirea unei fracții zecimale la un număr natural

Regula este următoarea:

Se împarte mai întâi partea întreagă la numărul dat și se scrie virgula la cât, apoi se continuă împărțirea ca la numere naturale, fără a ține cont de virgula de la deîmpărțit.

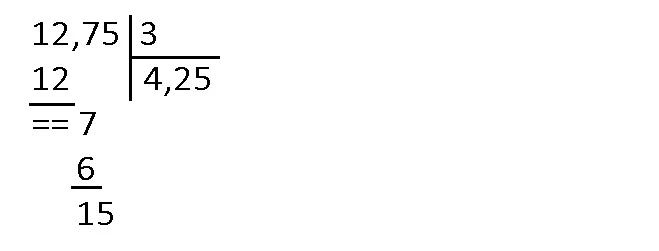
Împărțirea a două fracții zecimale cu număr finit de zecimale

Regula este următoarea:

Se înmulțesc cele două numere cu 10 sau 100 sau 1000 etc astfel încât împărțitorul să devină natural și apoi se efectueaza împărțirea între cele două numere astfel obținute.

Exemplu: Rezolvați împarțirea 22,5 : 0,15

0,15   100 = 15;    22,5  100 = 2250

2250 : 15 = 150

Deci 22,5 : 0,15 = 150.

Transformarea fracțiilor zecimale în fracții ordinare

Fracții zecimale cu număr finit de zecimale:

La numărător se scrie numărul fără virgulă, iar la numitor se scrie o putere a lui 10 cu exponent egal cu numărul de zecimale. (câte zecimale, atâtea zerouri după 1 la numitor)

Exemplul 1:

2,03 = 

203 este numărul fără virgula

100 este 10 la puterea a doua (exponentul puterii lui 10 este egal cu numărul de zecimale) – sau putem spune că avem atâtea zerouri după cifra 1, câte zecimale are fracția.

Exemplul 2:

0,005 = 

5 este numărul fără virgula

1000 este format din cifra 1 și trei de zero, pentru ca sunt 3 zecimale

Fracții zecimale periodice simple:

Se scrie la numărător numărul întreg, fără virgule, din care se scade numărul fără virgule format din cifrele din fața perioadei, iar la numitor, un număr format din atâtea cifre de 9 câte cifre are perioada.

Exemplul 1:

2,(6) = 

La numărător avem: 26, numărul fără virgulă minus 2 (numărul format din cifrele din fața perioadei)

9: avem o cifră în perioadă, așadar vom avea la numitor o cifra de 9

Exemplul 2:

5,(42) = 

La numărător avem: 542, numărul scris fără virgulă minus 5 (numărul format din cifrele din fața perioadei)

La numitor avem 99, deoarece avem două cifre în perioadă, deci două cifre de 9.

Fracții zecimale periodice mixte:

La numărător se scrie tot numărul, fără virgulă, cu tot cu perioadă, din care se scade numărul, fără virgule, format din cifrele dinaintea perioadei, iar la numitor, un număr format din atâtea cifre de 9 câte cifre are perioada și atâtea cifre de 0 câte zecimale sunt în fața perioadei.

Exemplu:

1,2(57)=

La numărător avem: 1257, numărul fără virgulă, minus 12 (numărul format din cifrele din fața perioadei)

La numitor avem: 990 (pentru două cifre în perioadă scriem doi de 9 și pentru o zecimală neperiodică scriem un 0)