Congruența triunghiurilor
Acest material despre congruența triunghiurilor cuprinde următoarele noțiuni: triunghiuri congruente, criterii de congruență a triunghiurilor oarecare (latură-latură-latură, latură-unghi-latură, unghi-latură-unghi), criterii de congruență a triunghiurilor dreptunghice (catetă-catetă, catetă-unghi ascuțit, ipotenuză-unghi ascuțit, ipotenuză-catetă), metoda triunghiurilor congruente.

Triunghiuri congruente
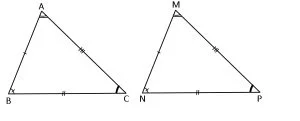
Două triunghiuri sunt congruente dacă au laturile și unghiurile respectiv congruente.
ΔABC≡ΔMNP <=>
m∢A = m∢M, m∢B = m∢N, m∢C = m∢P și AB=MN, BC=NP, CA=PM.
Criteriile de congruență ale triunghiurilor oarecare
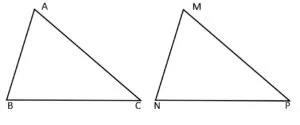
Criteriile de congruență ale triunghiurilor oarecare sunt următoarele:
L.L.L. (latură-latură-latură)
Dacă laturile unui triunghi sunt respectiv congruente cu laturile altui triunghi, atunci cele două triunghiuri sunt congruente.
AB=MN, BC=NP, CA=MP => (LLL) ΔABC≡ΔMNP
L.U.L. (latură-unghi-latură)
Dacă două laturi ale unui triunghi și unghiul dintre ele sunt respectiv congruente cu două laturi ale altui triunghi si unghiul dintre acelea, atunci cele două triunghiuri sunt congruente.
AB=MN, m∢B = m∢N, BC=NP => (LUL) ΔABC≡ΔMNP
U.L.U. (unghi-latură-unghi)
Dacă două unghiuri ale unui triunghi și latura dintre ele sunt respectiv congruente cu două unghiuri ale altui triunghi și latura dintre acelea, atunci cele două triunghiuri sunt congruente.
m∢A = m∢M, AB=MN, m∢B = m∢N => (ULU) ΔABC≡ΔMNP
Criteriile de congruență ale triunghiurilor dreptunghice
Criteriile de congruență ale triunghiurilor dreptunghice sunt următoarele:
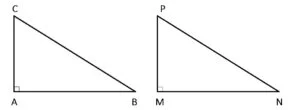
ΔABC: m∢A = 90°
ΔMNP: m∢M = 90°
C.C. (catetă-catetă)
Dacă două triunghiuri dreptunghice au catetele respectiv congruente, atunci cele două triunghiuri sunt congruente.
AB = MN, AC = MP => (CC) ΔABC≡ΔMNP
C.U. (catetă-unghi)
Dacă două triunghiuri dreptunghice au câte o catetă și unghiul ascuțit asociat acestora congruente, atunci cele două triunghiuri sunt congruente.
AB = MN, m∢B = m∢N => (CU) ΔABC≡ΔMNP
I.U. (ipotenuză-unghi)
Dacă două triunghiuri dreptunghice au ipotenuzele și câte un unghi ascuțit respectiv congruente, atunci cele două triunghiuri sunt congruente.
BC = NP, m∢B = m∢N => (CU) ΔABC≡ΔMNP
I.C. (ipotenuză-catetă)
Dacă două triunghiuri dreptunghice au ipotenuzele și câte o catetă respectiv congruente, atunci cele două triunghiuri sunt congruente.
AB = MN, BC = NP => (IC) ΔABC≡ΔMNP
Metoda triunghiurilor congruente
Metoda triunghiurilor congruente presupune stabilirea congruenței elementelor corespunzătoare a două triunghiuri, prin demonstrarea congruenței celor două triunghiuri, utilizându-se un criteriu de congruență.

