Mulțimea numerelor raționale
Acest material despre mulțimea numerelor raționale cuprinde următoarele noțiuni: definirea numărului rațional, proprietățile operațiilor cu numere raționale, modulul unui număr rațional, adunarea și scăderea numerelor raționale, înmulțirea și împărțirea numerelor raționale, puterea cu exponent întreg a unui număr rațional, reguli de calcul cu puteri ale numerelor raționale.

Definirea numărului rațional
ℚ={![]() | a,b ϵ Z, (a,b) = 1, bŧ0}
| a,b ϵ Z, (a,b) = 1, bŧ0}
Exemple:
-5 este număr rațional pentru că poate fi scris ca ![]() .
.
1,4 este rațional pentru că poate fi scris ca ![]()
Proprietățile operațiilor cu numere raționale
Dacă a,b ∈ ℚ, atunci a + b ∈ ℚ.
Dacă a,b ∈ ℚ, atunci a – b ∈ ℚ.
Dacă a,b ∈ ℚ, atunci a ∙ b ∈ ℚ.
Dacă a,b ∈ ℚ, atunci a : b ∈ ℚ.
Modulul unui număr rațional
Modulul unui număr rațional r se notează: |r|
|r| = +r, dacă r>0
|r| = 0, dacă r=0
|r| = -r, dacă r<0
Exemple:
|6,5| = +6,5
|-![]() | = -(-
| = -(-![]() ) = +
) = +![]()
Adunarea și scăderea numerelor raționale
Dacă numerele raționale sunt exprimate prin fracții ordinare, adunarea lor se face astfel:
- se aduc fracțiile la același numitor.
- se adună numărătorii, folosind regulile de adunare de la adunarea numerelor întregi.
Exemplu:
Ex: 4)![]() + (- 5)
+ (- 5)![]() ) =
) = ![]() =
= ![]() (3 =
(3 = ![]() .
.
Proprietățile adunării numerelor raționale (a,b,c numere raționale):
- comutativitate: a+b=b+a
- asociativitate (a+b)+c=a+(b+c)
- 0 este element neutru a+0=a
- a este opusul lui a și a+(-a)=0
Scăderea numereor raționale se realizează prin adunarea descăzutului cu opusul scăzatorului
Exemplu: (![]() )-
)- ![]() =(-
=(-![]() ) + (-
) + (-![]() )=
)=![]() =
= ![]()
Înmulțirea și împărțirea numerelor raționale
Pentru a înmulți două numere raționale, se înmulțesc modulele lor și se aplică regula semnelor, de la numere întregi:
(+)·(+) = (+)
(+)·(-) = (-)
(-)·(+) = (-)
(-)·(-) = (+)
Exemplu:
(-![]() ) · (+
) · (+![]() )=-(
)=-(![]() ·
· ![]() ) = –
) = –![]() = –
= –![]()
Pentru a împărți două numere raționale, se împart modulele lor și se aplică regula semnelor, de la numere întregi:
(+):(+) = (+)
(+):(-) = (-)
(-):(+) = (-)
(-):(-) = (+)
Proprietățile înmulțirii numerelor raționale (a,b,c numere raționale):
- comutativitate: a·b=b·a
- asociativitate (a·b)·c=a·(b·c)
- 1 este element neutru a·1=a
 =
= 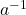 este inversul lui a (a≠0)
este inversul lui a (a≠0)- a·
 =1
=1 - distributivitatea față de adunare și scădere a·(b±c)=a·b±a·c
Puterea cu exponent întreg a unui număr rațional
![]() =r·r·…·r (n ori), adică r înmulțit cu el însuși de n ori (r = număr rațional, n= număr natural, n nenul)
=r·r·…·r (n ori), adică r înmulțit cu el însuși de n ori (r = număr rațional, n= număr natural, n nenul)
Exemplu: (0,5)![]() = 0,5 · 0,5 = 0,25
= 0,5 · 0,5 = 0,25
![]() =1 (rϵQ*)
=1 (rϵQ*)
Exemplu: ![]() =1
=1
![]() =r (rϵQ)
=r (rϵQ)
Exemplu: ![]() =
=![]()
![]() =0 (mϵZ)
=0 (mϵZ)
Exemplu: ![]() = 0.
= 0.
![]() nu are sens.
nu are sens.
![]() =
= ![]() (rϵQ, nϵN*)
(rϵQ, nϵN*)
Exemplu: ![]() =
=![]() =
=![]() =
=![]() =
=![]()
Reguli de calcul cu puteri ale numerelor raționale
(a,b ϵQ*, x,y ϵZ)
![]()
Exemplu: ![]()
![]()
Exemplu: ![]()
![]()
Exemplu: [![]() ]
]![]() =
=![]()
![]()
Exemplu: ![]()
![]()
Exemplu: 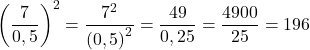
Aplicabilitate mulțimea numerelor raționale
Mulțimea numerelor raționale este o colecție de numere care pot fi exprimate ca raportul dintre două numere întregi. Această mulțime include atât numere întregi, cât și fracții.
Un exemplu de aplicație a numerelor raționale este în calculul cu fracții. De exemplu, în matematică sau științe, avem adesea nevoie să efectuăm operații cu fracții, cum ar fi adunarea, scăderea, înmulțirea și împărțirea. Pentru a face acest lucru, trebuie să folosim numere raționale.
O altă aplicație importantă a numerelor raționale este în reprezentarea valorilor zecimale exacte. Multe numere zecimale, cum ar fi 0,5 sau 0,25, pot fi reprezentate ca fracții în baza 10. Acestea sunt exemple de numere raționale.
În plus, numerele raționale sunt utilizate și în geometrie, deoarece pot reprezenta mărimi fizice sau distanțe între puncte.
Să luăm ca exemplu o aplicație din fizică. Când calculăm viteza medie a unui obiect care se deplasează pe o anumită distanță într-un anumit interval de timp, trebuie să efectuăm operații cu fracții. Aceasta se face prin împărțirea distanței parcurse de obiect la timpul necesar pentru a parcurge acea distanță, iar rezultatul este un număr rațional.
În concluzie, mulțimea numerelor raționale are multe aplicații practice în știință, matematică și alte domenii, fiind o componentă importantă în reprezentarea și calculul valorilor precise și în efectuarea operațiilor matematice.

