Operații cu numere reale 📚

Operații cu numere reale

Acest material despre operații cu numere reale cuprinde următoarele noțiuni: modulul unui număr real, adunarea și scăderea numerelor reale, înmulțirea și împărțirea numerelor reale, puterea unui număr real cu exponent întreg, raționalizarea numitorilor de forma $a\sqrt{b}$ , media aritmetică a n numere reale, media aritmetică ponderată a n numere reale, media geometrică a două numere reale și ecuația de forma =a.

Modulul unui număr real:

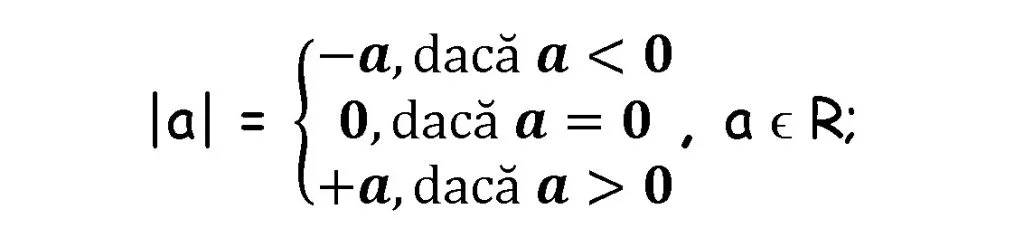
Exemple:

|- $\sqrt{7}$ | = – (- $\sqrt{7}$ ) = $\sqrt{7}$

|+ $2\sqrt{3}$ | = + $2\sqrt{3}$

| $3\sqrt{2} - 5$ | = | $\sqrt{18} - \sqrt{25}$ | = -( $\sqrt{18} - \sqrt{25}$ ) = – $\sqrt{18} + \sqrt{25}$ = – $3\sqrt{2} + 5$

Adunarea și scăderea numerelor reale

Dacă a,b ϵ R atunci a+b ϵ R și a-b ϵ R.

Dacă termenii cuprind același radical, se scad/adună numerele din fața radicalului:

$a\sqrt{c}$ ± $b\sqrt{c}$ = (a ± b) $\sqrt{c}$

Exemplu: $2\sqrt{3} + 4\sqrt{3}$ = $(2+4)\sqrt{3}$ = $6\sqrt{3}$

Dacă termenii nu cuprind același radical, se lasă sub forma unei sume/diferențe de numere iraționale:

Exemplu: $2\sqrt{2}$ + $3\sqrt{5}$ rămâne scris așa.

Înmulțirea și împărțirea numerelor reale

Dacă a,b ϵ R atunci a·b ϵ R și $\frac{a}{b}$ ϵ R. (b nenul)

$x\sqrt{a}\cdot y\sqrt{b} = xy\sqrt{ab}$

Exemplu: $2\sqrt{5}\cdot 3\sqrt{10} = 2\cdot 3\sqrt{5\cdot 10} = 6\sqrt{50} = 6\cdot5\sqrt{2} = 30\sqrt{2}$

$\dfrac{x\sqrt{a}}{y\sqrt{b}} = \dfrac{x}{y}\cdot\sqrt{\dfrac{a}{b}}$ , b,y nenule.

Exemplu: $\dfrac{6\sqrt{15}}{3\sqrt{5}} = \dfrac{6}{3}\cdot\sqrt{\dfrac{15}{5}} = 2\sqrt{3}$

Puterea unui număr real cu expoent întreg:

Dacă a ϵ R, p ϵ Z, atuci $a^p$ ϵ R.

( $a\sqrt{b}$ ) $^n$ = $a^n\cdot\sqrt{b^n}$ , a,b ϵ R, b≥0, n ϵ Z.

Exemplu: ( $2\sqrt{3}$ ) $^4$ = $2^4\cdot\sqrt{3^4}$ = $16\cdot 3^2$ = $16\cdot 9$ = $144$ .

( $\sqrt{a}$ ) $^2^n$ = $a^n$

Exemplu: $\sqrt{2}^6 = 2^3$

( $\sqrt{a}$ ) $^2^n^+^1$ = ( $a^n$ ) $\sqrt{a}$ , a≥0, nϵ N.

Exemplu: ( $\sqrt{5}$ ) $^7$ = ( $5^3$ ) $\sqrt{5}$

Raționalizarea numitorului de forma 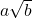$a\sqrt{b}$

$\dfrac{^\sqrt{c}) a}{b\sqrt{c}} = \dfrac{a\sqrt{c}}{bc}$ , c>0

Exemplu: $\dfrac{^\sqrt{2}) 3}{5\sqrt{2}} = \dfrac{3\sqrt{2}}{5\cdot 2} = \dfrac{3\sqrt{2}}{10}$

Media aritmetică a n numere reale:

$m_a(a_1,a_2,...,a_n) = \dfrac{a_1+a_2+...+a_n}{n}$

Exemplu:

Un elev are notele 9, 5 și 7 la istorie. Care este media notelor sale?

$m_a = \dfrac{9+5+7}{3} = \dfrac{21}{3} = 7$

Media aritmetică ponderată a n numere reale

$m_a_p = \dfrac{a_1\cdot p_1+a_2\cdot p_2+...+a_n\cdot p_n}{p_1+p_2+...+p_n}$

Exemplu:

Într-o firma exista doi angajați cu salariu de 2500 lei, trei au salariul 3000 lei și un angajat are 4000 lei. Determinați salariul mediu din firma respectivă.

$m_a_p = \dfrac{2500\cdot 2+3000\cdot 3+4000\cdot 1}{2+3+1} = \dfrac{18000}{6} = 3000 lei$

Media geometrică a două numere reale pozitive a și b

$m_g(a,b) = \sqrt{ab}$

Exemplu:

Media geometrică a numerelor 2 și 4 este:

$m_g(2,4) = \sqrt{2\cdot 4} = \sqrt{8} = 2\sqrt{2}$

Ecuația de forma 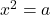$x^2 = a$ , a ϵ R

a) Dacă a ϵ R, a< 0, atunci nu există soluții reale.

b) Dacă a ϵ R, a≥0, atunci:

Soluția este: S = { $-\sqrt{a},+\sqrt{a}$ },

Exemplu: Ecuația $x^2 = 7$ , are soluțiile:

x = $-\sqrt{7}$ sau

x = $+\sqrt{7}$

Operații cu numere reale în viața reală

Numerele reale sunt omniprezente în viața noastră de zi cu zi, iar efectuarea operațiilor cu acestea este esențială în multe domenii practice, cum ar fi economia, construcțiile, gătitul sau sportul. Iată câteva exemple din viața reală care ilustrează utilizarea operațiilor cu numere reale:

1. Adunarea și scăderea numerelor reale

Exemplu: O familie merge la cumpărături și își calculează bugetul. Ei au de cheltuit 120 de lei și cumpără următoarele produse:

Fructe: 25,40 lei
Lactate: 38,20 lei
Pâine și alte produse de panificație: 17,80 lei

Totalul este:
$25,40 + 38,20 + 17,80 = 81,40 \ \text{lei}$

Pentru a afla cât le mai rămâne din buget:
$120 – 81,40 = 38,60 \ \text{lei}$
Astfel, le rămân 38,60 lei pentru alte cheltuieli.

2. Înmulțirea numerelor reale

Exemplu: Un om de afaceri participă la un târg unde vinde 150 de produse, fiecare la prețul de 7,80 lei. Pentru a calcula venitul total, trebuie să înmulțească numărul produselor cu prețul unitar:
$150 \cdot 7,80 = 1170 \ \text{lei}$
Venitul total al afaceristului este de 1170 de lei.

3. Împărțirea numerelor reale

Exemplu: O persoană își planifică o excursie de 6 zile, având un buget total de 2400 de lei pentru cazare. Pentru a calcula cât poate cheltui pe zi, împarte bugetul total la numărul de zile:
$2400 \div 6 = 400 \ \text{lei/zi}$
Astfel, persoana știe că nu trebuie să cheltuiască mai mult de 400 de lei pe noapte pentru cazare.

4. Ridicarea la putere și rădăcina pătrată

Exemplu: Un arhitect proiectează o grădină pătrată și știe că suprafața acesteia trebuie să fie de 100 m². Pentru a calcula lungimea laturii grădinii, aplică formula rădăcinii pătrate:
$l = \sqrt{100} = 10 \ \text{m}$
Lungimea laturii grădinii este de 10 metri.

Dacă dorește să dubleze suprafața acesteia (200 m²), ridică lungimea inițială la pătrat:
$10^2 = 100 \ \text{m}^2$

Concluzie

Folosirea operațiilor cu numere reale ne ajută să planificăm bugete, să organizăm activități sau să realizăm proiecte complexe. Deși învățăm aceste operații în școală, ele sunt instrumente fundamentale pe care le folosim zilnic, adesea fără să ne dăm seama.

Dacă îți place platforma noastră, te invit și pe pagina noastră de Facebook și Youtube

Meniu

Operații cu numere reale

Modulul unui număr real:

Adunarea și scăderea numerelor reale

Înmulțirea și împărțirea numerelor reale

Puterea unui număr real cu expoent întreg:

Raționalizarea numitorului de forma $a\sqrt{b}$

Media aritmetică a n numere reale:

Media aritmetică ponderată a n numere reale

Media geometrică a două numere reale pozitive a și b

Ecuația de forma $x^2 = a$ , a ϵ R

Operații cu numere reale în viața reală

1. Adunarea și scăderea numerelor reale

2. Înmulțirea numerelor reale

3. Împărțirea numerelor reale

4. Ridicarea la putere și rădăcina pătrată

Concluzie

Meniu

Link-uri utile

ANPC

Meniu

Operații cu numere reale

Modulul unui număr real:

Adunarea și scăderea numerelor reale

Înmulțirea și împărțirea numerelor reale

Puterea unui număr real cu expoent întreg:

Raționalizarea numitorului de forma

Media aritmetică a n numere reale:

Media aritmetică ponderată a n numere reale

Media geometrică a două numere reale pozitive a și b

Ecuația de forma , a ϵ R

Operații cu numere reale în viața reală

1. Adunarea și scăderea numerelor reale

2. Înmulțirea numerelor reale

3. Împărțirea numerelor reale

4. Ridicarea la putere și rădăcina pătrată

Concluzie

Meniu

Link-uri utile

ANPC

Raționalizarea numitorului de forma $a\sqrt{b}$

Ecuația de forma $x^2 = a$ , a ϵ R