Perimetre și arii
Acest material despre arii și perimetre cuprinde următoarele noțiuni: perimetriul și aria triunghiului, perimetrul și aria paralelogramului, perimetrul și aria dreptunghiului, perimetrul și aria rombului, perimetrul și aria pătratului, precum și perimetrul și aria trapezului.

Perimetrul și aria triunghiului
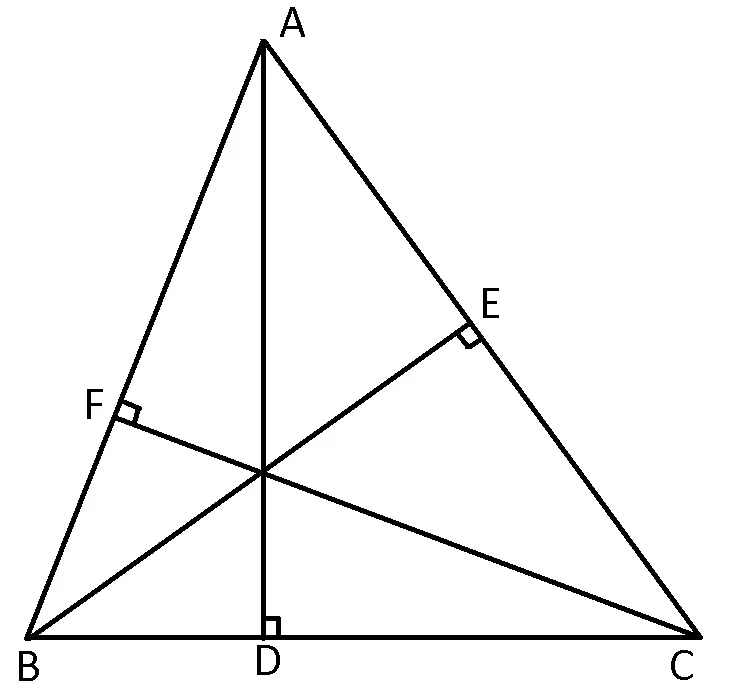
Perimetrul unui triunghi este egal cu suma lungimilor laturilor triunghiului.
P ABC=AB+BC+CA
ABC=AB+BC+CA
Aria unui triunghi este egală cu jumătatea produsului dintre lungimea unei laturi a triunghiului (denumită bază) și lungimea înălțimii corespunzătoare laturii.
A ABC=
ABC=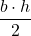 =
= 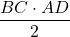 =
= 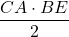 =
= 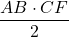
Aria triunghiului dreptunghic
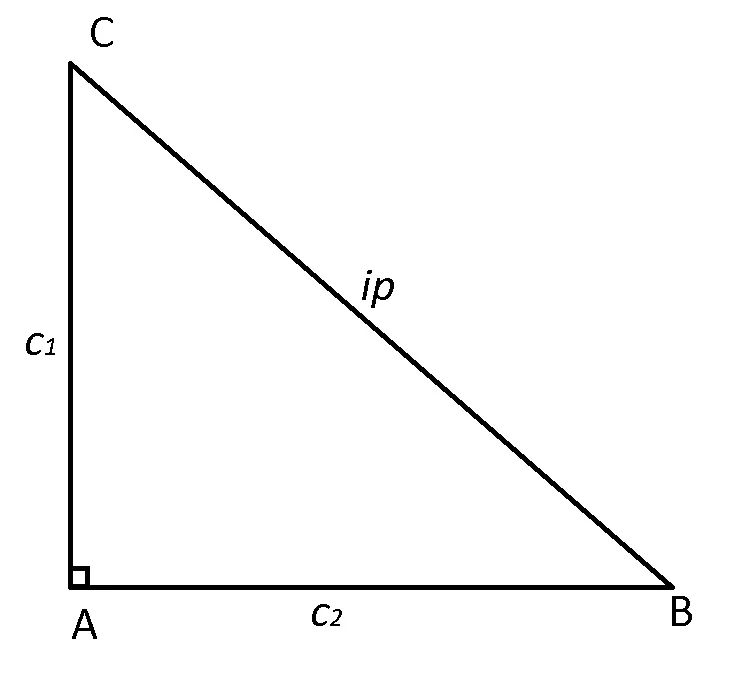
A ABC=
ABC=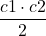 =
= 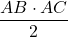
Perimetrul și aria paralelogramului
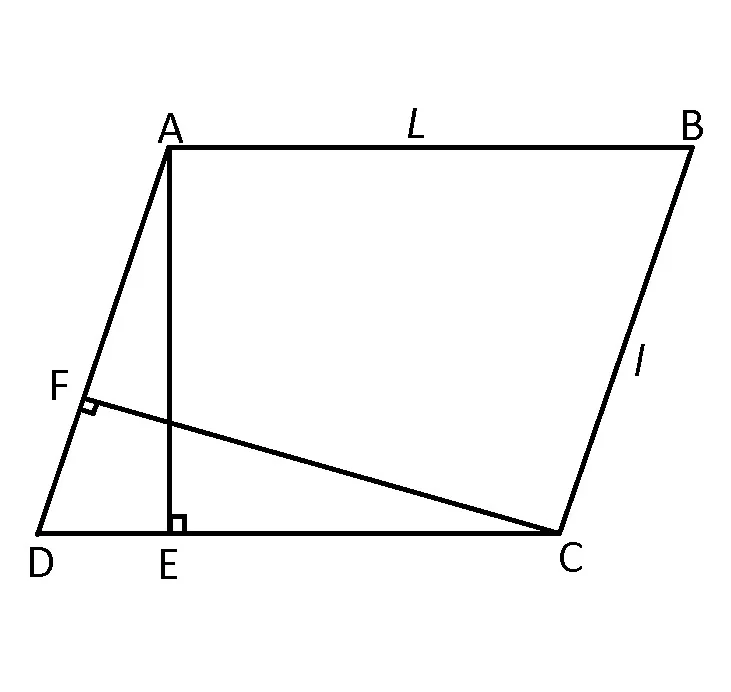
Perimetrul unui paralelogram este egal cu suma dintre dublul lungimii și dublul lățimii.
PABCD=2L + 2l = 2(AB+BC)
Aria unui paralelogram este egală cu produsul dintre lungimea unei laturi și lungimea înălțimii corespunzătoare acesteia.
AABCD= =
= 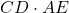 =
= 
Perimetrul și aria dreptunghiului
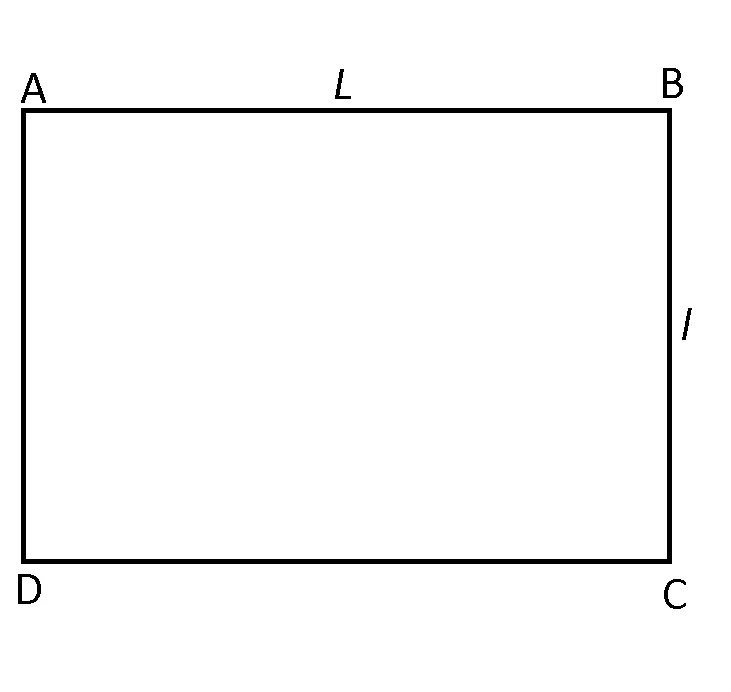
Perimetrul unui dreptunghi este egal cu suma dintre dublul lungimii și dublul lățimii.
PABCD=2L + 2l = 2(AB+BC)
Aria unui dreptunghi este egală cu produsul dintre lungime și lățime.
AABCD=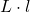 =
= 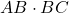
Perimetrul și aria rombului
Perimetrul unui romb este egal cu suma celor patru laturi.
PABCD=4l = 4AB
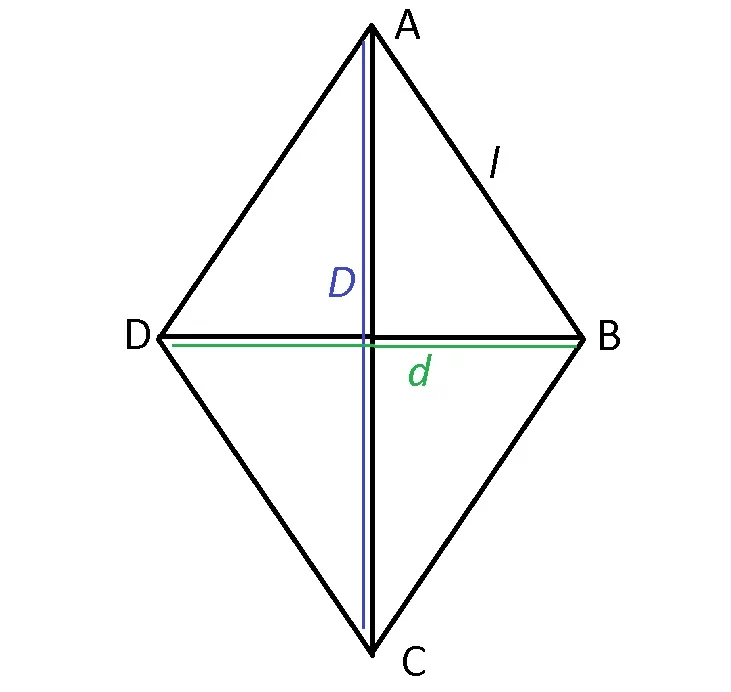
Aria unui romb este egală cu jumătatea produsului diagonalelor sale.
AABCD=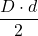 =
= 
Perimetrul și aria pătratului
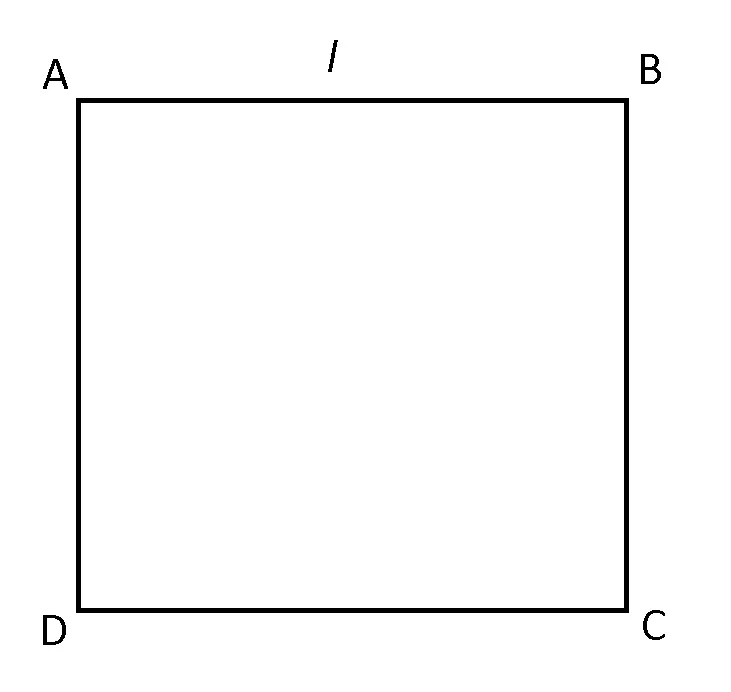
Perimetrul unui pătrat este egal cu suma celor patru laturi.
PABCD=4l = 4AB
Aria unui pătrat este egală cu pătratul laturii sale.
AABCD=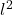 =
= 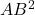
Perimetrul și aria trapezului
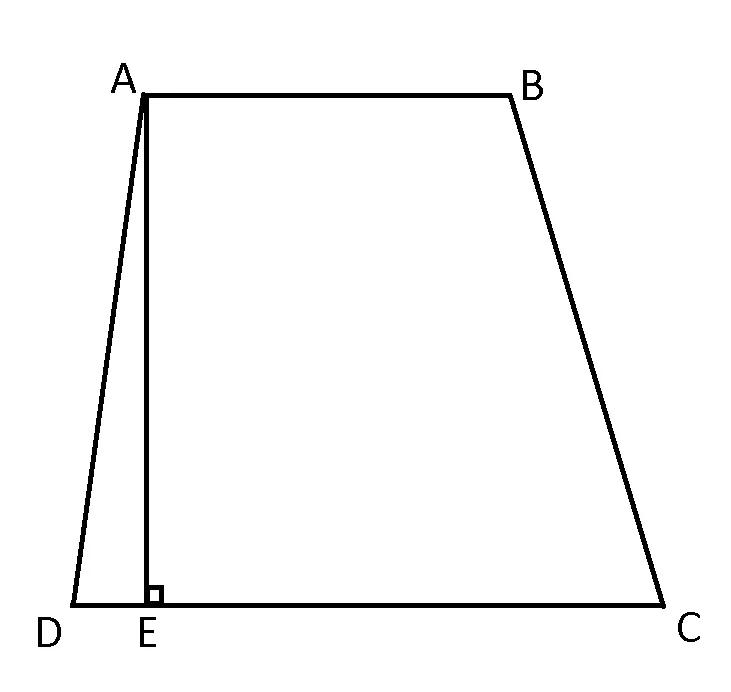
Perimetrul unui trapez este egal cu suma lungimilor laturilor trapezului.
PABCD=AB+BC+CD+DA
Aria unui trapez este egală cu jumătatea produsului dintre suma bazelor și înălțimea trapezului.
AABCD=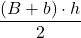 =
= 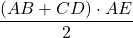
Utilizarea în viața reală, Perimetre și arii: Importanța în Diverse Domenii
Perimetrul și aria sunt două concepte fundamentale în geometrie și matematică, cu o varietate de aplicații practice în viața de zi cu zi și în domenii precum construcțiile, designul, agricultura, urbanismul și multe altele. Aceste concepte, în ciuda naturii lor abstracte, sunt esențiale pentru înțelegerea și rezolvarea unor probleme practice.
Utilizarea Perimetrelor:
Perimetrul este suma lungimilor tuturor laturilor unei forme geometrice, cum ar fi un dreptunghi, un pătrat sau un cerc. În viața reală, conceptul de perimetru este adesea folosit în următoarele moduri:
Construcții și Arhitectură: În domeniul construcțiilor, perimetrul este esențial pentru calcularea cantității de material necesar pentru marginile structurilor, cum ar fi gardurile, fundațiile sau terasele. De asemenea, este folosit pentru evaluarea dimensiunilor exterioare ale unei clădiri sau a unei camere.
Amenajarea Grădinilor: În grădinărit, cunoașterea perimetrelor este importantă pentru a determina cât de mult gard este necesar pentru a înconjura o grădină sau pentru a calcula lungimea unei vii pe care doriți să o plantați în jurul grădinii.
Înțelegerea Terenului: În domeniul agricol, agricultorii calculează perimetrul câmpurilor pentru a estima cât de mult gard este necesar pentru a proteja culturile de animale sau pentru a îngrădi terenurile agricole.
Calcularea Costurilor: În domeniul financiar, perimetrul poate fi folosit pentru a estima costurile asociate cu îngrădirea proprietății, cum ar fi costul gardului sau prețul de instalare a gardului.
Utilizarea Ariilor:
Aria este mărimea spațiului închis de către o formă geometrică. Este o măsură a suprafeței, exprimată în unități pătrate (de exemplu, metri pătrați, centimetri pătrați, acri etc.). În viața reală, aria este folosită într-o varietate de moduri practice:
Construcții și Design Interior: În domeniul construcțiilor și designului interior, aria este folosită pentru a calcula cantitatea de material necesar pentru a acoperi o anumită suprafață, cum ar fi parchetul, gresia sau tapetul.
Agricultură și Horticultură: Fermierii calculează aria câmpurilor și a grădinilor pentru a estima cantitatea de semințe sau de pesticide necesare pentru a acoperi terenurile. De asemenea, aria este folosită pentru a determina randamentul culturilor și pentru a planifica spațiile de cultivare.
Urbanism și Dezvoltare Imobiliară: În planificarea urbană, aria este esențială pentru a determina densitatea locuințelor, spațiile verzi și alte facilități publice. De asemenea, este folosită pentru a calcula impozitele pe proprietate și pentru a evalua valoarea terenurilor.
Înțelegerea Ecologică: În domeniul ecologic, aria este utilizată pentru a măsura și monitoriza habitatul speciilor, pentru a evalua impactul defrișărilor sau urbanizării asupra mediului înconjurător și pentru a planifica conservarea resurselor naturale.
În concluzie, perimetre și arii sunt concepte matematice fundamentale cu o gamă largă de aplicații practice în viața reală. De la construcții și agricultură la urbanism și ecologie, aceste concepte sunt esențiale pentru înțelegerea și soluționarea unor probleme complexe din diverse domenii. O înțelegere solidă a acestor concepte este crucială pentru progresul și dezvoltarea societății moderne.

