Relații metrice în triunghiul dreptunghic
Acest material despre Relații metrice în triunghiul dreptunghic include următoarele noțiuni: proiecții ortogonale pe o dreaptă, teorema înălțimii, teorema catetei, teorema lui Pitagora, reciproca teoremei lui Pitagora, noțiuni de trigonometrie în triunghiul dreptunghic.

Proiecții ortogonale pe o dreaptă
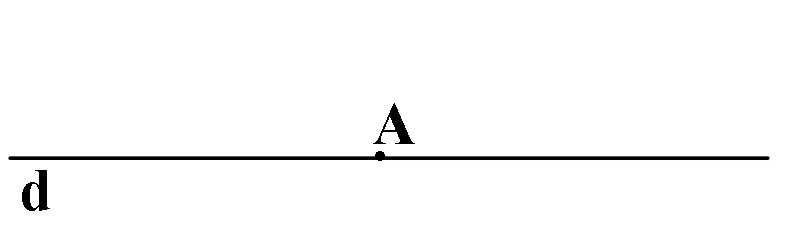
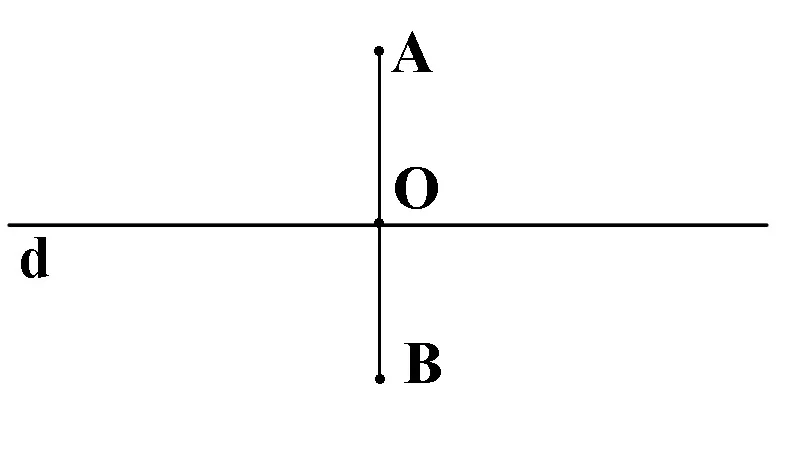
Proiecția ortogonală a unui punct A pe o dreaptă d reprezintă piciorul perpendicularei duse din punctul A pe dreapta d.
Dacă A ∉ d: prdA=A’, unde AA’⊥d, A’∈ d:

Dacă A ∈ d: prdA=A
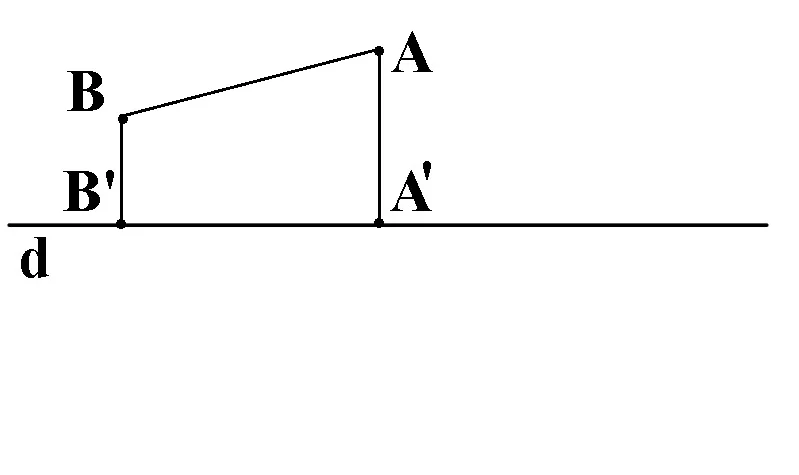
Proiecția ortogonală a unui segment AB pe o dreaptă d reprezinta segmentul care cuprinde proiecțiile tuturor punctelor de pe segmentul AB pe dreapta d.
Dacă AB nu este perpendicular pe d, A,B ∉ d, atunci prdAB=A’B’, unde A’= prdA, B’= prdB.
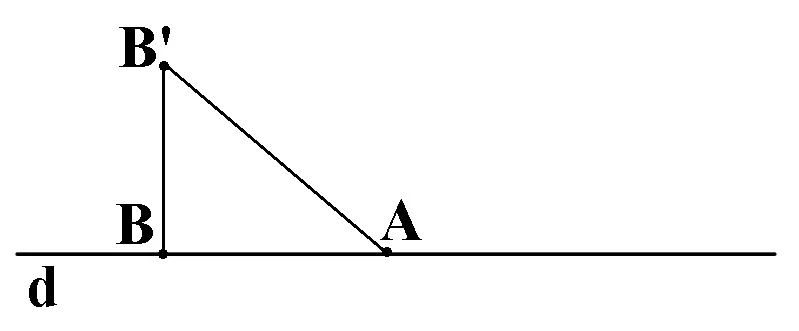
Dacă AB nu este perpendicular pe d, A ∈ d,B ∉ d, atunci prdAB=AB’, unde unde B’= prdB.
Dacă AB ⊥ d, atunci prdAB=O unde AB ∩ d = {O}.
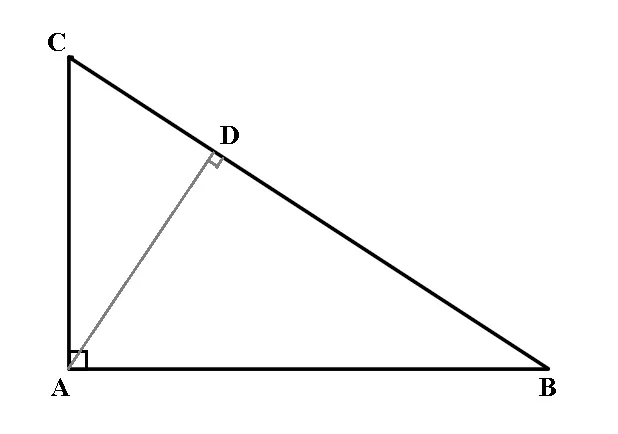
Teorema înălțimii
Într-un triunghi dreptunghic, lungimea înălțimii care pleacă din vârful unghiului drept este medie geometrică între lungimile proiecțiilor catetelor pe ipotenuză.
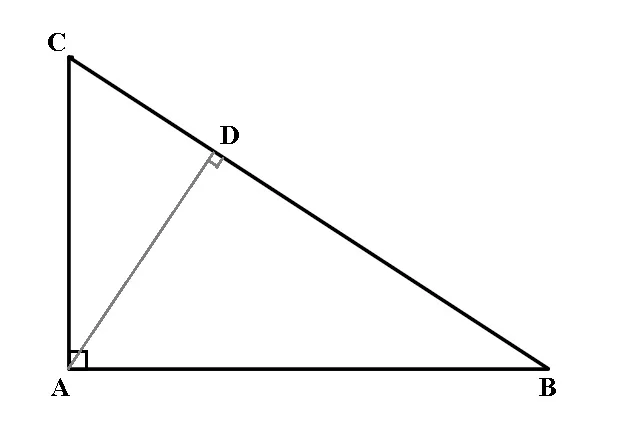
ΔABC cu m∢A = 90°, dacă AD⊥BC, D∈BC, atunci:
AD = ![]() sau
sau
AD2=BD ∙ CD
Reciproca teoremei înălțimii
Dacă într-un triunghi ABC, care nu este triunghi obtuzunghic, lungimea înălțimii AD este media geometrică a lungimilor proiecțiilor laturilor AB și AC pe BC, atunci acel triunghi este dreptunghic.
ΔABC cu m∢A ≤ 90°, m∢B ≤ 90°, m∢C ≤ 90°, dacă AD = ![]() sau AD2=BD ∙ CD, atunci:
sau AD2=BD ∙ CD, atunci:
m∢A = 90°
Teorema catetei
Într-un triunghi dreptunghic, lungimea unei catete este medie geometrică între lungimea ipotenuzei și lungimea proiecției respectivei catete pe ipotenuză.

ΔABC cu m∢A = 90°, dacă AD⊥BC, D∈BC, atunci:
AB = ![]() sau AB2=BC ∙ BD și
sau AB2=BC ∙ BD și
AC = ![]() sau AC2=BC ∙ CD
sau AC2=BC ∙ CD
Reciproca teoremei catetei
Dacă într-un triunghi ABC, cu D=prBCA și D∈B, avem: AB2=BC ∙ BD sau AC2=BC ∙ CD, atunci m∢A = 90°.
Teorema lui Pitagora
Într-un triunghi dreptunghic, pătratul lungimii ipotenuzei este egal cu suma pătratelor lungimilor catetelor.
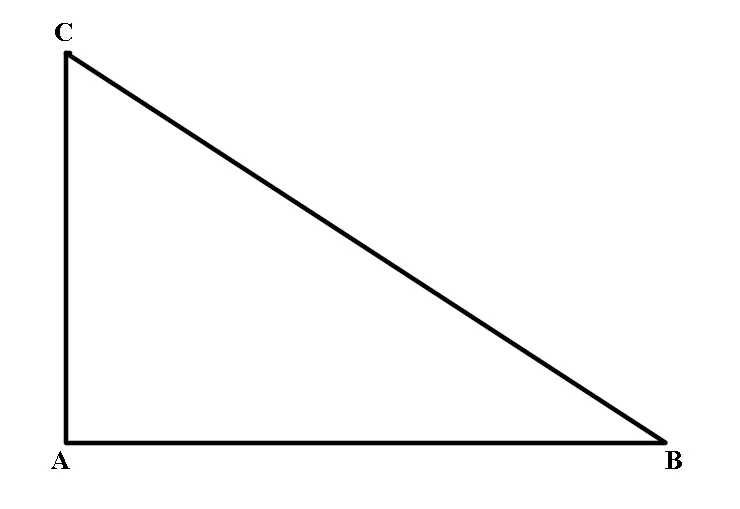
În ΔABC cu m∢A = 90°, BC2 = AB2 + AC2.
Reciproca teoremei lui Pitaora
Dacă, într-un triunghi, pătratul lungimii unei laturi este suma pătratelor celorlalte două laturi, atunci triunghiul este dreptunghic, unghiul drept fiind cel opus primei laturi.
Dacă, într-un triunghi ABC are loc relația BC2 = AB2 + AC2, atunci ΔABC dreptunghic cu m∢A = 90°.
Noțiuni de trigonometrie în triunghiul dreptunghic
Fie ΔABC cu m∢A:

Sinusul unui unghi ascuțit al unui triunghi dreptunghic:
sinus = ![]()
sin B = ![]()
sin C = ![]()
Cosinusul unui unghi ascuțit al unui triunghi dreptunghic:
cosinus = ![]()
cos B = ![]()
cos C = ![]()
Tangenta unui unghi ascuțit al unui triunghi dreptunghic:
tangenta = ![]()
tg B = ![]()
tg C = ![]()
Cotangenta unui unghi ascuțit al unui triunghi dreptunghic:
cotangenta = ![]()
ctg B = ![]()
ctg C = ![]()
| Măsura unghiului: | 30° | 45° | 60° |
| sin: | |||
| cos: | |||
| tg: | 1 | ||
| ctg: | 1 |
Relații metrice în triunghiul dreptunghic – Aplicații practice din viața reală
Triunghiul dreptunghic joacă un rol crucial în matematică, iar relațiile metrice asociate acestuia ne sunt extrem de utile în activitățile cotidiene și diverse profesii. Formulele din geometrie, precum teorema lui Pitagora sau rapoartele trigonometrice, sunt aplicate în numeroase contexte reale. Iată câteva exemple practice:
1. Calcularea înălțimii unei clădiri sau a unui obiect inaccesibil
Imaginând o clădire ca fiind înaltă , cu o umbră de lungime cunoscută, iar unghiul de elevație al Soarelui fiind , putem folosi tangenta unghiului dintr-un triunghi dreptunghic format:
De exemplu, dacă lungimea umbrei este de 10 metri, iar unghiul Soarelui este de 45°, putem calcula înălțimea astfel:
2. Determinarea distanței peste un obstacol
Dacă o persoană dorește să măsoare distanța peste un râu fără să traverseze, poate folosi un teodolit. Își alege un punct fix pe malul opus și măsoară unghiurile și distanțele folosind teorema lui Pitagora.
De exemplu, dacă distanța de la observator la baza triunghiului este de 20 metri, iar distanța înaltă este de 15 metri:
Înlocuind valorile:
3. Construcții și proiectare
Constructorii utilizează relațiile metrice pentru a verifica dacă unghiurile dintr-o structură sunt drepte. Cu ajutorul teoremei lui Pitagora:
pot confirma corectitudinea unui dreptunghi sau a unui colț al unei clădiri. Dacă, de exemplu, diagonala unei camere dreptunghiulare trebuie să fie de 5 metri, iar laturile sunt de 3 metri și 4 metri, putem verifica:
Rezultatul fiind corect, unghiul este drept.
4. Navigație și GPS
Dispozitivele GPS folosesc triunghiuri dreptunghice pentru a calcula distanțele și pozițiile pe suprafața globului. De exemplu, dacă trebuie să ajungi la un punct în linie dreaptă , cunoscând distanța est-vest () și nord-sud (), aplicația folosește relațiile:
5. Înclinația rampelor
Calculul unghiurilor și lungimii unei rampe pentru persoanele cu dizabilități implică tangenta unghiului dintre rampă și orizontală:
Dacă o rampă urcă 1 metru () și baza sa () este de 5 metri, unghiul de înclinare se poate calcula ca:
6. Arhitectură și design
Un designer care creează structuri geometrice poate folosi relațiile metrice pentru a calcula diagonalele panourilor. Dacă are un dreptunghi de lățime 2 metri și lungime 3 metri, lungimea diagonalei () se determină astfel:
Aceste exemple ilustrează că relațiile metrice din triunghiurile dreptunghice nu sunt doar concepte teoretice, ci soluții utile în construcții, navigație, design și multe alte domenii. Ele ne oferă uneltele necesare pentru a înțelege spațiul și distanțele din lumea reală.

