Elemente de organizare a datelor 📚

Elemente de organizare a datelor

Acest material despre elemente de organizare a datelor cuprinde următoarele teme: produsul cartezian a două mulțimi nevide, sistemul de axe ortogonale și dependențe funcționale.

Produsul cartezian a două mulțimi nevide

Fie A și B două mulțimi nevide.

Produsul cartezian al mulțimilor A și B ne notează A X B și reprezintă mulțimea perechilor (a,b), cu proprietatea ca a este element al mulțimii A și b este element al mulțimii B.

A X B = {(a,b)/ a∈A, b∈B}

Numărul elementelor produsului cartezian a două mulțimi: card(A X B) = card(A) ⋅ card(B)

Exemplu:

Fie A = {1,2}, B={3,4,5}

A X B = {(1,3), (1,4), (1,5), (2,3), (2,4), (2,5)}.

card(A X B) = card(A) ⋅ card(B) = 2 ⋅ 3 = 6.

Sistemul de axe ortogonale

Sistemul de axe ortogonale (Reperul cartezian) reprezintă o pereche ordonată de axe perpendiculare și se notează, de regulă, cu xOy.

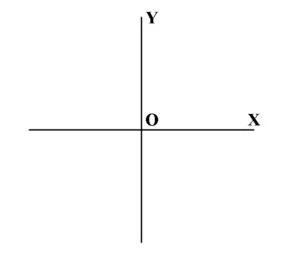
Originea sistemului de axe ortogonale este originea celor două axe și se notează cu O (punctul de intersecție a celor două axe).

Axa absciselor reprezintă axa orizontală și se notează cu Ox. Se parcurge de la stânga la dreapta.

Axa ordonatelor reprezintă axa verticală și se notează cu Oy. Se parcurge de jos în sus.

Fiecărei perechi de numere reale (x,y) îi corespunde un punct unic în plan, care se reprezintă astfel:

valoarea lui x se reprezintă pe axa orizontală, astfel se marcheaza un punct pe axa Ox
valoarea lui y se reprezintă pe axa verticală, astfel se marcheaza un punct pe axa Oy
Se desenează un dreptunghi cu vârfurile în O, punctul marcat pe Ox și punctul marcat pe Oy.
Cel de-al patrulea vârf al dreptunghiului reprezintă punctul unic de coordonate (x,y).

Exemplu:

Punctul A(-2,3) se reprezintă astfel:

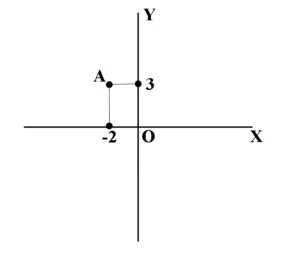
Punctul A este reprezentarea geometrică a perechii de numere reale (-2,3).

Numerele reale -2 și 3 sunt coordonatele punctului A.

Primua coordonată, -2, este coordonata orizontală, sau abscisa, și se notează cu xA. Avem xA = -2.

Cea de-a doua coordonată, 3, este coordonata verticală, sau ordonata, și se notează cu yA. Avem yA = 3.

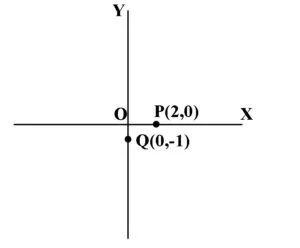
Un punct situat pe axa orizontală Ox are ordonata nulă. Exemplu: P(2,0) ∈ Ox

Un punct cituat pe axa verticală Oy are abscisa nulă. Exemplu: Q(0,-1) ∈ Oy

Distanța dintre două puncte

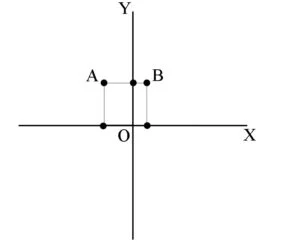
Două puncte A și B sunt situate pe aceeași dreaptă orizontală dacă au aceeași ordonată: yA = yB

Distanța dintre două puncte A și B situate pe aceeași dreaptă orizontală este AB = |xB – xA|

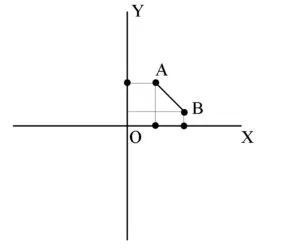
Exemplu: Punctele A(-2,3) și B(1,3) sunt situate pe aceeași dreaptă orizontală pentru ca yA = yB = 3.

Distanța dintre A și B este AB = |xB – xA| = |1- (-2)| = |3| =3.

Două puncte A și B sunt situate pe aceeași dreaptă verticală dacă au aceeași abscisă: xA = xB

Distanța dintre două puncte A și B situate pe aceeași dreaptă verticală este AB = |yB – yA|

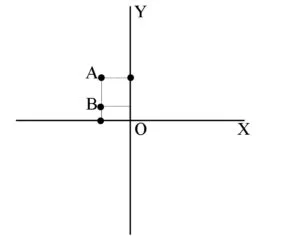
Exemplu: Punctele A(-2,3) și B(-2,1) sunt situate pe aceeași dreaptă verticală pentru ca xA = xB = -2.

Distanța dintre A și B este AB = |yB – yA| = |1- 3| = |-2| =2.

Distanța dintre două puncte A(x_A, y_A) și B(x_B, y_B) este:

AB = $\sqrt{\left(XB - XA\right)^2 + \left (YB-YA\right)^2}$

Exemplu:

Distanța dintre punctele A(2,3) și B(4,1) este:

AB = $\sqrt{\left(4 - 2\right)^2 + \left (1-3\right)^2}$ = $\sqrt{2^2 + \left (-2\right)^2}$ = $\sqrt{4+ 4}$ = $\sqrt{8}$ = 2 $\sqrt{2}$

Dependențe funcționale

Spunem că, între două mulțimi nevide A și B există o dependență funcțională dacă, printr-o regulă oarecare, fiecărui element din mulțimea A îi corespunde un unic element din mulțimea B.

Exemplu:

Fie A = {1,2,3,4,5}

B = {2,3,4,5,6,7}

și relația y=x+1.

Între mulțimile A și B există o dependență funcțională y=x+1, dacă, atribuindu-i lui x fiecare valoare din A, obținem o valoare unică y care se regăsește în mulțimea B.

Pentru x=1∈A, y=1+1=2∈B

Pentru x=2∈A, y=2+1=3∈B

Pentru x=3∈A, y=3+1=4∈B

Pentru x=4∈A, y=4+1=5∈B

Pentru x=5∈A, y=5+1=6∈B.

Așadar , între mulțimile A și B există o dependență funcțională y=x+1.

Exemple din viața reală ale produsului cartezian, sistemului de axe ortogonale și dependențelor funcționale

Matematica teoretică găsește adesea aplicabilitate în viața de zi cu zi, iar conceptele precum produsul cartezian, sistemul de axe ortogonale și dependențele funcționale au numeroase utilizări practice. Acestea ne permit să înțelegem relații între date, să reprezentăm informații în spațiu și să identificăm legături cauzale.

1. Produsul cartezian al două mulțimi nevide

Produsul cartezian al două mulțimi $\text{A} \times \text{B}$ este setul format din toate perechile ordonate posibile $(a, b)$ , unde $a \in \text{A}$ și $b \in \text{B}$ .

Exemplu: Organizarea unei competiții sportive

Să presupunem că într-o competiție există două grupe de echipe:
$\text{A} = \{\text{E1, E2}\}$ , $\text{B} = \{\text{E3, E4}\}$ . Produsul cartezian $\text{A} \times \text{B}$ reprezintă toate meciurile posibile între echipe din grupe diferite:

$\text{A} \times \text{B} = \{(\text{E1}, \text{E3}), (\text{E1}, \text{E4}), (\text{E2}, \text{E3}), (\text{E2}, \text{E4})\}.$

Această metodă este utilizată și pentru programarea întâlnirilor sau calcularea combinațiilor posibile într-un turneu.

Exemplu suplimentar: Meniuri personalizate

La un restaurant, produsul cartezian poate fi folosit pentru a combina feluri principale ( $\text{A}$ ) cu băuturi ( $\text{B}$ ):

$\text{A} = \{\text{Pizza, Salată}\}, \text{B} = \{\text{Apă, Suc}\}.$

Toate opțiunile clienților:

$\text{A} \times \text{B} = \{(\text{Pizza}, \text{Apă}), (\text{Pizza}, \text{Suc}), (\text{Salată}, \text{Apă}), (\text{Salată}, \text{Suc})\}.$

2. Sistemul de axe ortogonale

Sistemul de axe ortogonale este esențial pentru reprezentarea grafică a datelor și analizarea acestora.

Exemplu: Hărțile și navigația

Un GPS folosește un sistem de coordonate pentru a indica poziția unui utilizator pe o hartă. Fiecare punct este identificat printr-un set de coordonate $(x, y)$ , unde:

$x$ reprezintă poziția est-vest,
$y$ reprezintă poziția nord-sud.

Astfel, folosind coordonatele, hărțile oferă o reprezentare grafică clară, iar punctele de interes sunt ușor localizate.

Exemplu: Analiza economică

Graficul cererii și ofertei este un exemplu tipic:

Axa $x$ : cantitatea de produse,
Axa $y$ : prețul.
Intersecția curbelor de cerere și ofertă arată prețul de echilibru.

3. Dependențele funcționale

O dependență funcțională este o relație în care valorile unei variabile (sau mulțimi de date) determină valorile altei variabile.

Exemplu: Calculul facturilor la utilități

În cazul energiei electrice, costul facturii depinde direct de consumul de kWh:

$\text{Cost} = \text{Preț per kWh} \times \text{Consum}.$

Dacă prețul este constant la 0,50 lei/kWh, consumul determină valoarea finală a facturii.

Exemplu: Salarizarea angajaților

Un exemplu de dependență funcțională este calculul salariilor:

$\text{Salariu brut} = \text{Ore lucrate} \times \text{Tarif orar}.$

Dacă un angajat lucrează 40 de ore la un tarif de 50 de lei/oră, salariul său brut va fi de:

$40 \times 50 = 2000 \, \text{lei}.$

Exemplu suplimentar: Agricultura

În agricultură, producția este influențată de suprafața cultivată:

$\text{Recoltă} = \text{Randament pe hectar} \times \text{Număr de hectare}.$

Aceste concepte – produsul cartezian, sistemele de axe ortogonale și dependențele funcționale – demonstrează cât de importantă este matematica în organizarea și interpretarea datelor pentru rezolvarea problemelor din viața de zi cu zi. Fie că planificăm o competiție sportivă, navigăm cu ajutorul unui GPS sau gestionăm resurse financiare și materiale, aceste instrumente matematice ne fac viața mai eficientă.

Dacă îți place platforma noastră, te invit și pe pagina noastră de Facebook și Youtube

Meniu