Funcții
Acest material despre funcții cuprinde următoarele noțiuni: noțiunea de funcție, imaginea unei funcții, graficul unei funcții și funcții numerice, funcții de forma f : D → ℝ, f(x) = ax +b, unde a, b ∈ ℝ, iar D ⊂ ℝ sau D = ℝ reprezentarea grafică a unei funcții de forma f : ℝ → ℝ, f(x) = ax +b, unde a, b ∈ ℝ

Noțiunea de funcție
Fie două mulțimi nevide A și B. Dacă, printr-un procedeu oarecare, îi atribuim fiecărui element din mulțimea A un singur element din mulțimea B, spunem că definim funcția f pe mulțimea A cu valori în mulțimea B.
Notație:
f : A → B (citim: funcția f, definită pe A cu valori în B)
Mulțimea A se numește: domeniu de definiție
Mulțimea B se numește: codomeniu (mulțimea în care ia valori funcția)
Procedeul f se numește: lege de coresondență
Dacă unui element x din mulțimea A îi corespunde un unic element y din mulțimea B, printr-o lege de corespondență f, spunem ca valoarea funcției f în x este y și scriem: f(x)=y.
În funcție de modalitatea în care este dată legea de corespondență, o funcție poate fi reprezentată prin:
- Diagrama;
- Tabel;
- O expresie algebrică
- Mai multe expresii algebrice
Exemplificăm mai jos:
Diagramă:
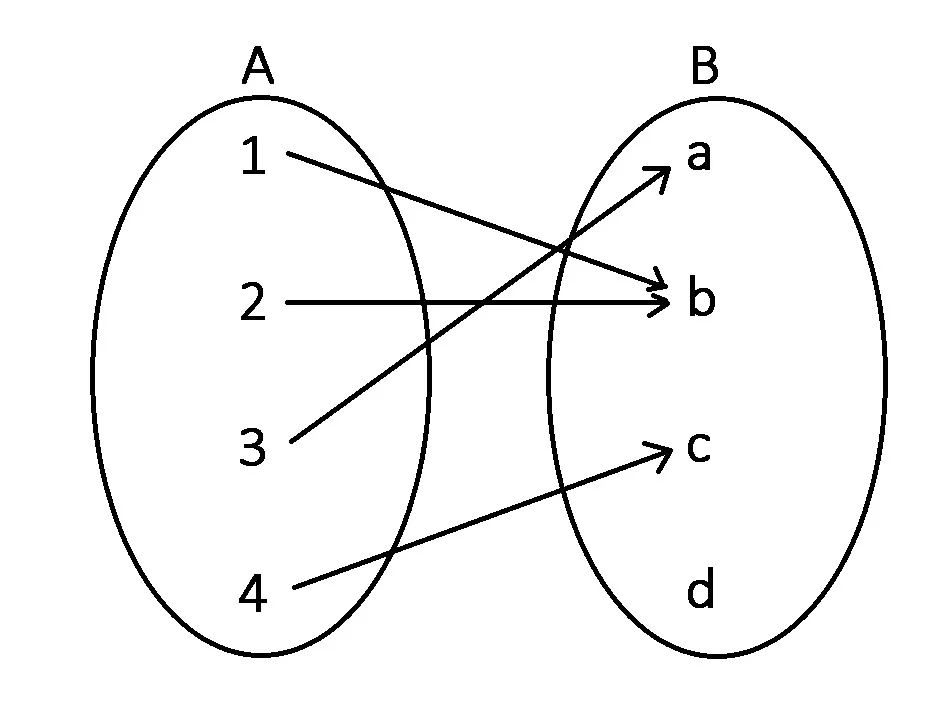
Tabel:
| x | 2 | 3 | 5 | 7 |
| f(x) | 4 | 6 | 10 | 14 |
Expresie algebrică:
f : ℝ → ℝ
f(x) = 5x + 3
Mai multe expresii algebrice:
f : ℝ → ℝ
f(x) = 2x, pentru x ∈ ( -∞, 0)
f(x) = 3x – 1, pentru x ∈ [0, +∞)
Imaginea unei funcții
Fie f : A → B
Imaginea funcției f reprezintă mulțimea tuturor valorilor pe care le poate lua funcția f și se notează Imf.
Imf = {f(x) | x ∈ A}
Exemplu:
f : {1,2,3} → ℝ
f(x) = x+1
f(1) = 1+1 = 2
f(2) = 2+1 = 3
f(3) = 3+1 = 4
Așadar Imf = {2,3,4}
Graficul unei funcții.
Funcții numerice
Graficul unei funcții f : A → B se notează Gf și reprezintă mulțimea definită astfel:
Gf = {(x, y), x ∈ A, y ∈ B, y = f(x)}
O funcție f : A → B este o funcție numerică dacă toate elementele din A și B sunt numere reale.
Altfel spus, f : A → B este o funcție numerică dacă A ⊂ ℝ și B ⊂ ℝ sau A = B = ℝ.
Exemplu de funcție numerică:
f : (1,2) → ℝ, f(x) = x+1.
Reprezentarea geometrică a graficului funcției f constă în mulțimea tuturor punctelor de coordonate x și y, unde f(x) = y.
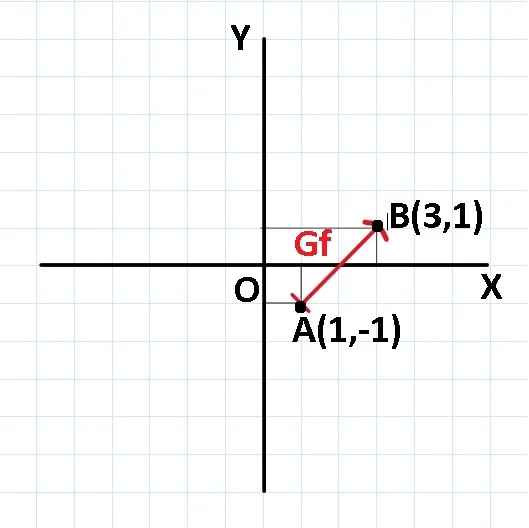
Exemplu:
f : {1,3} → ℝ;
f(1) = -2,
f(3) = 2.
Avem Gf = {A(1,-2), B(3,2)}
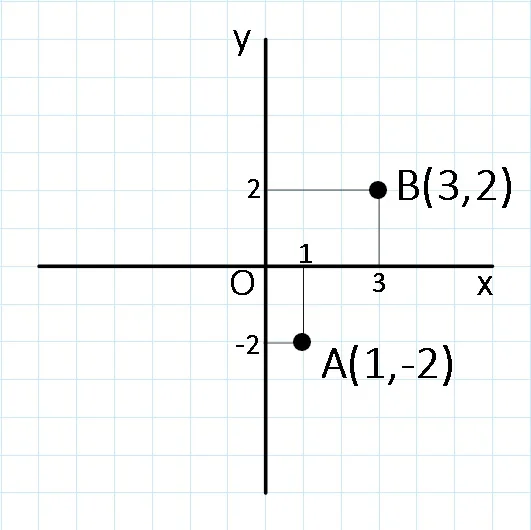
Funcții de forma f : D → ℝ, f(x) = ax + b, unde a, b ∈ ℝ, iar D ⊂ ℝ sau D = ℝ
Fie f : ℝ → ℝ, f(x) = ax + b. a,b ∈ ℝ.
Dacă a=0, atunci f(x) = b și f este o funcție constantă.
Exemplu de funcție constantă: f : ℝ → ℝ, f(x) = -3.
Dacă a≠0, atunci f(x) = ax + b și f este o funcție de gradul I.
Exemplu de funcție de gradul I: f : ℝ → ℝ, f(x) = 2x – 4.
Reprezentarea grafică a funcției de forma f : ℝ → ℝ, f(x) = ax + b, unde a, b ∈ ℝ
Graficul unei funcții de forma f : ℝ → ℝ, f(x) = ax + b, unde a, b ∈ ℝ este o dreaptă.
Modalități de reprezentare a graficului unei funcții de forma f : ℝ → ℝ, f(x) = ax + b, unde a, b ∈ ℝ
- Identificarea a două puncte distince, aleatorii, de pe graficul funcției f.
- Identificarea punctelor reprezentând intersecția graficului funcției f cu axele de coordonate din sistemul xOy.
Exemplu:
f : ℝ → ℝ, f(x) = 2x – 4
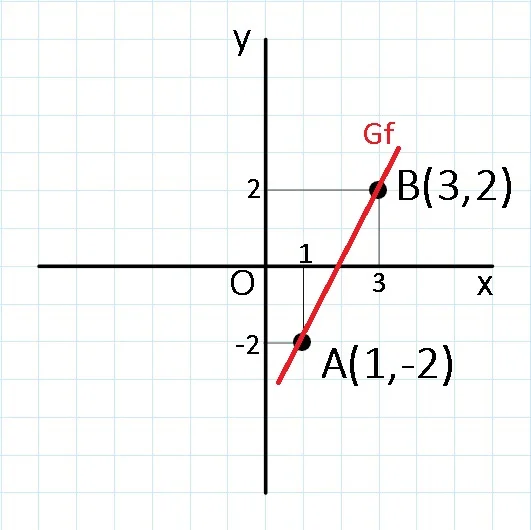
Modalitatea 1: Identificarea a două puncte distince, aleatorii, de pe graficul funcției f.
Alegem, în mod aleatoriu, două valori pentru x:
Pentru x = 1:
f(1) = 2⋅ 1 – 4
f(1) = -2.
Avem punctul A(1,-2).
Pentru x = 3:
f(3) = 2⋅ 3 – 4
f(3) = 2.
Avem punctul B(3,2).
Reprezentăm punctele A și B în sistemul de coordonate xOy.
Graficul funcției f este dreapta care trece prin punctele A și B.
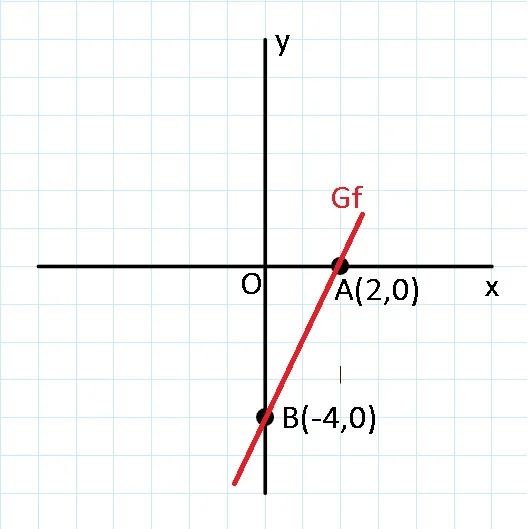
Modalitatea 2: Identificarea punctelor reprezentând intersecția graficului funcției f cu axele de coordonate din sistemul xOy
Pentru intersecția graficului funcției f cu axa de coordonate Ox, se egalează f(x) cu 0 și se calculează x.
Gf ∩ Ox:
f(x) = 0
2x – 4 = 0
Deci 2x – 4 = 0
Obținem x = 2.
Așadar f(2) = 0. Avem punctul A(2,0).
Pentru intersecția graficului funcției f cu axa de coordonate Oy, se egalează x cu 0 și se calculează f(0).
Gf ∩ Oy:
x = 0
f(0) = 2⋅ 0 – 4
Așadar f(0) = -4. Avem punctul B(0,-4).
Graficul funcției f este dreapta care trece prin punctele A și B.
Cum verificăm dacă un punct aparține graficului unei funcții?
Punctul M(m,n) se află pe graficul funcției f : ℝ → ℝ, f(x) = ax + b, unde a, b ∈ ℝ, dacă f(m) = n.
Exemple:
f : ℝ → ℝ, f(x) = x + 5.
Punctul M(2,7) ∈ Gf pentru că f(2) = 2+5 = 7.
Punctul N(-1,-4) ∉ Gf, pentru că f(-1) = -1+5 = 4 ≠ -4.
Reprezentarea graficului unei funcții de forma f : D → ℝ, f(x) = ax + b, unde a, b ∈ ℝ, D ⊂ ℝ
Pentru a reprezenta grafic o funcție f : [p,q] → R, f(x) = ax + b, unde a, b ∈ ℝ, trebuie reprezentate grafic punctele P(p, f(p)) și Q(q, f(q)). Graficul funcției va fi segmentul PQ. Punctele P și Q aparțin graficului funcției.
Pentru a reprezenta grafic o funcție f : [p,q) → R, f(x) = ax + b, unde a, b ∈ ℝ, trebuie reprezentate grafic punctele P(p, f(p)) și Q(q, f(q)). Graficul funcției va fi segmentul PQ. Punctul P aparține graficului funcției, iar punctul Q nu aparține graficului funcției.
Pentru a reprezenta grafic o funcție f : (p,q] → R, f(x) = ax + b, unde a, b ∈ ℝ, trebuie reprezentate grafic punctele P(p, f(p)) și Q(q, f(q)). Graficul funcției va fi segmentul PQ. Punctul P nu aparține graficului funcției, iar punctul Q aparține graficului funcției.
Pentru a reprezenta grafic o funcție f : (p,q) → R, f(x) = ax + b, unde a, b ∈ ℝ, trebuie reprezentate grafic punctele P(p, f(p)) și Q(q, f(q)). Graficul funcției va fi segmentul PQ. Punctele P și Q nu aparțin graficului funcției.
Pentru a reprezenta grafic o funcție f : [p,+∞) → R, f(x) = ax + b, unde a, b ∈ ℝ, trebuie reprezentate grafic punctul P(p, f(p)) și încă un punct Q(q, f(q)). Graficul funcției va fi semidreapta (PQ. Punctele P și Q aparțin graficului funcției.
Pentru a reprezenta grafic o funcție f : (p,+∞) → R, f(x) = ax + b, unde a, b ∈ ℝ, trebuie reprezentate grafic punctul P(p, f(p)) și încă un punct Q(q, f(q)). Graficul funcției va fi semidreapta (PQ. Punctul P nu aparține graficului funcției, iar Q aparține graficului funcției.
Pentru a reprezenta grafic o funcție f : (-∞, q] → R, f(x) = ax + b, unde a, b ∈ ℝ, trebuie reprezentate grafic un punct P(p, f(p)) și punctul Q(q, f(q)). Graficul funcției va fi semidreapta (QP. Punctele P și Q aparțin graficului funcției.
Pentru a reprezenta grafic o funcție f : (-∞, q)→ R, f(x) = ax + b, unde a, b ∈ ℝ, trebuie reprezentate grafic punctul P(p, f(p)) și încă un punct Q(q, f(q)). Graficul funcției va fi semidreapta (PQ. Punctul P aparține graficului funcției, iar Q nu aparține graficului funcției.
Exemplu:
f : [1,3) → R, f(x) = x – 2.
f(1) = -1, deci avem P(1, -1)
f(3) = 1, deci avem Q(3, 1).
Graficul funcției f este segmentul PQ. P aparține graficului funcției, Q nu aparține graficului funcției.
Utilizare Funcții
Funcțiile matematice sunt concepte fundamentale care descriu relații între elemente din diferite seturi de date. Ele sunt utilizate într-o varietate de domenii, de la științe și inginerie până la economie și tehnologie, având aplicații practice în viața de zi cu zi. În acest articol, vom explora câteva dintre modurile în care funcțiile matematice sunt utilizate în practică.
1. Finanțe și Economie
În domeniul finanțelor și economiei, funcțiile matematice sunt utilizate pentru a modela și analiza fenomene complexe, precum evoluția prețurilor, ratele de dobândă sau comportamentul piețelor financiare. De exemplu, funcțiile exponențiale sunt utilizate pentru a descrie creșterea sau scăderea exponențială a valorilor în timp, iar funcțiile logaritmice sunt folosite pentru a calcula ratele de creștere sau de scădere a unei cantități în funcție de timp.
Cunoștințele despre funcțiile matematice sunt esențiale pentru analiza datelor financiare și pentru luarea deciziilor informate în ceea ce privește investițiile, economisirea sau gestionarea riscurilor. Aceste informații ajută managerii financiari, economiștii și investitorii să înțeleagă și să prevadă tendințele pieței și să optimizeze strategiile lor financiare.
2. Științe și Inginerie
În domeniul științelor și ingineriei, funcțiile matematice sunt utilizate pentru a modela și rezolva probleme legate de fenomene fizice și naturale. De exemplu, ecuațiile diferențiale sunt folosite pentru a descrie și a rezolva probleme de mișcare, de difuzie sau de transfer de căldură în fizică și inginerie. De asemenea, funcțiile trigonometrice sunt utilizate pentru a descrie fenomene periodice, precum oscilațiile undelor sau mișcarea corpurilor astronomice.
Cunoștințele despre funcțiile matematice sunt esențiale pentru proiectarea și optimizarea sistemelor și proceselor din diverse domenii, cum ar fi ingineria civilă, ingineria electrică sau biologia. Aceste informații ajută inginerii și cercetătorii să înțeleagă și să modeleze fenomenele naturale și să dezvolte soluții inovatoare pentru provocările complexe ale lumii moderne.
3. Tehnologie și Calculatoare
În domeniul tehnologiei și calculatoarelor, funcțiile matematice sunt utilizate pentru a dezvolta algoritmi și aplicații software care să rezolve diverse probleme și să optimizeze procesele. De exemplu, funcțiile de hashing sunt utilizate pentru a cripta și a securiza datele în aplicațiile de securitate cibernetică, iar funcțiile de interpolare sunt folosite pentru a analiza și a procesa datele în aplicațiile de prelucrare a imaginilor sau a sunetelor.
Cunoștințele despre funcțiile matematice sunt esențiale pentru dezvoltarea și implementarea tehnologiilor avansate și a aplicațiilor software care să satisfacă nevoile și cerințele utilizatorilor din întreaga lume. Aceste informații ajută dezvoltatorii și inginerii software să creeze produse și servicii inovatoare, care să aducă beneficii tangibile societății și economiei globale.
Concluzie
Funcțiile matematice sunt instrumente puternice și versatile care au o varietate de aplicații practice în viața reală, de la finanțe și economie până la științe și tehnologie. Utilizarea acestor funcții în diverse domenii contribuie la rezolvarea problemelor complexe și la dezvoltarea soluțiilor inovatoare pentru provocările lumii moderne. Prin urmare, este important să recunoaștem importanța și relevanța funcțiilor matematice și să le integrăm în mod corespunzător în practica noastră cotidiană pentru a facilita progresul și inovația în diferite domenii.

