Matrice. Tabel matriceal. Mulțimi de matrice
În ceea ce urmeaza, vă voi prezenta noțiuni despre Matrice. Tabel matriceal. Mulțimi de matrice, noțiuni ce se învață în clasa a 11a.
Definiție.
Fie ![]() . Se numește o matrice de tip (m,n) cu elemente numere complexe, o funcție
. Se numește o matrice de tip (m,n) cu elemente numere complexe, o funcție ![]() ,
, ![]() .
.
Elementele ![]() se numesc elementele matricei A.
se numesc elementele matricei A.
Matricea ![]() poate fi reprezentată sub formă de tablou dreptunghiular cu
poate fi reprezentată sub formă de tablou dreptunghiular cu ![]() linii și
linii și ![]() coloane, ca mai jos:
coloane, ca mai jos: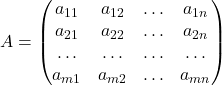
Exemple:
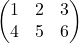 este o matrice tip (2,3) (are 2 linii și 3 coloane)
este o matrice tip (2,3) (are 2 linii și 3 coloane)
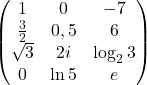 este o matrice tip (3,4) (are 3 linii și 4 coloane)
este o matrice tip (3,4) (are 3 linii și 4 coloane)
Notații: ![]() =mulțimea matricelor de m linii și n coloane cu elemente numere complexe (similar se folosesc notațiile
=mulțimea matricelor de m linii și n coloane cu elemente numere complexe (similar se folosesc notațiile ![]() ,
, ![]() ,
, ![]() și
și ![]() ).
).
Definiții:
1. Dacă m=1, atunci matricea se numește matrice linie.
Exemplu: ![]()
2. Dacă n=1, atunci matricea se numește matrice coloană.
Exemplu:
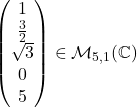
3. Dacă m=n, atunci matricea se numește matrice pătratică de ordin n, iar mulțimea tuturor acestor matrice se notează cu ![]() (respectiv
(respectiv ![]() ,
, ![]() ,
, ![]() sau
sau ![]() ).
).
Exemple:
![]() (matrice pătratică de ordin 2), iar
(matrice pătratică de ordin 2), iar 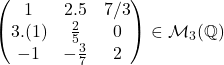 (matrice pătratică de ordin 3).
(matrice pătratică de ordin 3).
Definiție: Fie ![]() . Elementele
. Elementele ![]() formează diagonala principală a matricei
formează diagonala principală a matricei ![]() .
.
Suma acestor elemente se numește urma matricei ![]() și se notează
și se notează ![]() .
.
Exemplu:
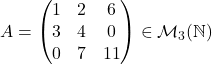 are ca diagonală principală elementele (1,4,11), iar urma matricei
are ca diagonală principală elementele (1,4,11), iar urma matricei ![]() este
este ![]() .
.
Utilizare matrice. Tabel matriceal. Mulțimi de matrice

Matematica este una dintre cele mai puternice și ubiquitare discipline științifice din lume, cu aplicații într-o varietate impresionantă de domenii. Unul dintre conceptele matematice fundamentale este reprezentat de tabelele matriciale și matricele. Acestea sunt utilizate pe scară largă în multe aspecte ale vieții noastre de zi cu zi, deși nu ne dăm adesea seama de prezența lor.
Utilizarea în viața de zi cu zi a Tabel matriceal. Matrice. Mulțimi de matrice.
Chiar dacă pare că matricele sunt concepte matematice abstracte, ele sunt folosite în mod frecvent în viața noastră de zi cu zi, inclusiv în următoarele domenii:
- Tehnologia informației: În tehnologia informației, matricele sunt esențiale în procesul de codificare și decodificare a informațiilor, în special în cadrul algoritmilor de criptare și decodare. Ele sunt, de asemenea, utilizate în compresia datelor, procesarea imaginilor și redarea video.
- Grafică computerizată și jocuri: În industria jocurilor video și a graficii computerizate, matricele sunt utilizate pentru a modela și transforma obiecte în spațiul 3D, pentru a aplica efecte vizuale și pentru a simula interacțiunile cu mediul virtual.
- Economie și finanțe: În analiza financiară, matricele sunt folosite pentru a rezolva sisteme de ecuații și pentru a calcula rate de schimb valutar, randamente ale investițiilor și alte mărimi economice relevante.
- Transport și logistică: În domeniul transportului, matricele sunt utilizate pentru a modela rețele de rute și pentru a calcula cele mai eficiente trasee pentru transportul bunurilor și persoanelor.
- Matematică aplicată: Matematica aplicată în știință și inginerie folosește matricele pentru a rezolva probleme complexe, cum ar fi simulările în fizică, inginerie electrică, optimizare și analiza datelor.
Aceste exemple dovedesc că matricele sunt o unealtă puternică și versatilă în multe domenii ale vieții noastre. Prin înțelegerea lor și aplicarea în contexte practice, putem rezolva probleme complexe și ne putem îmbunătăți abilitățile în diverse domenii de activitate.

