Legi de compoziție
Acest material despre legi de compoziție cuprinde următoarele noțiuni: definiție, exemple, proprietăți și se studiază în clasa a 12a.

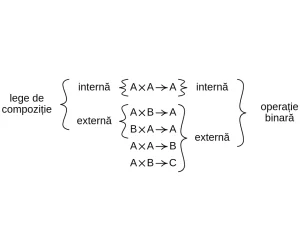
Definiție:
Fie 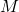 o mulțime nevidă. O funcție (aplicație)
o mulțime nevidă. O funcție (aplicație) 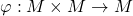 ,
, 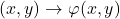 (perechii
(perechii 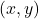 i se asociază valoarea
i se asociază valoarea 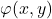 ) se numește lege de compoziție sau operație algebrică pe mulțimea
) se numește lege de compoziție sau operație algebrică pe mulțimea 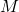 . (în loc de
. (în loc de 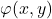 se poate folosi notația
se poate folosi notația 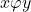 )
)
Exemple:
- Operațiile de adunare și înmulțire pe mulțimile de numere
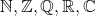
- Operațiile de adunare și înmulțire pe mulțimile de matrice
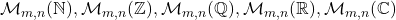
- Operația de adunare a vectorilor din plan
Observație: Operația de adunare se notează cu +, iar cea de înmulțire cu  .
.
Exemplu. 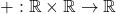 ,
, 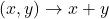 (operația de adunare pe mulțimea numerelor reale)
(operația de adunare pe mulțimea numerelor reale)
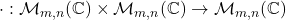 ,
, 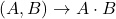 (operația de înmulțire a matricelor de tip
(operația de înmulțire a matricelor de tip 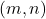 de numere complexe)
de numere complexe)
Se pot defini legi de compoziție și folosind mai multe operații algebrice. (acestea se pot nota prin semnele *,  ,
, 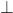 , T, etc)
, T, etc)
Exercițiu. Se dau legile de compoziție 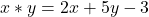 și
și 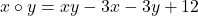 .
.
a. Calculați i).  , ii).
, ii). 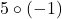 și iii).
și iii). 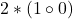 .
.
b. Rezolvați în 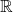 inecuația
inecuația 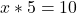 .
.
c. Rezolvați în 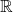 ecuația
ecuația 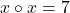 .
.
Rezolvare:
a. i). 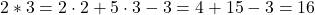 (se înlocuiește în legea de compoziție
(se înlocuiește în legea de compoziție 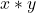 ,
, 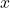 cu 2 și
cu 2 și 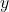 cu 3)
cu 3)
ii). 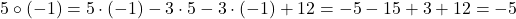 (se înlocuiește în legea de compoziție
(se înlocuiește în legea de compoziție 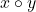 ,
, 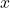 cu 5 și
cu 5 și 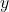 cu -1)
cu -1)
iii). 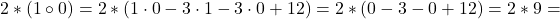
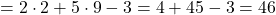 (se rezolvă mai întâi în interiorul parantezei)
(se rezolvă mai întâi în interiorul parantezei)
b. 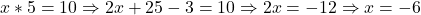 .
.
c. 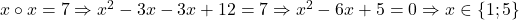 .
.
Proprietăți:
Parte stabilă
Definiție: Fie legea de compoziție 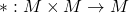 . O submulțime
. O submulțime  se numește parte stabilă a mulțimii M în raport cu legea de compoziție „*” dacă
se numește parte stabilă a mulțimii M în raport cu legea de compoziție „*” dacă 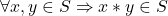 .
.
Pentru cazul particular 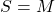 spunem că
spunem că 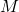 este parte stabilă în raport cu legea de compoziție „*”.
este parte stabilă în raport cu legea de compoziție „*”.
Exemple:
1. Fie 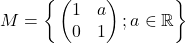 și operația de înmulțire a matricelor. Atunci
și operația de înmulțire a matricelor. Atunci 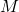 este parte stabilă în raport cu operația de înmulțire, deoarece
este parte stabilă în raport cu operația de înmulțire, deoarece 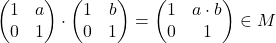 ,
, 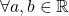 .
.
2. Să considerăm operația de scădere pe mulțimea 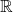 . Mulțimea
. Mulțimea 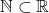 nu este parte stabilă în raport cu scăderea, deoarece pentru numerele naturale 3 și 7, avem
nu este parte stabilă în raport cu scăderea, deoarece pentru numerele naturale 3 și 7, avem 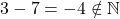 (se pot găsi și
(se pot găsi și
Comutativitate
Definiție: O lege de compoziție 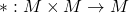 este comutativă dacă
este comutativă dacă 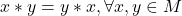 .
.
Exercițiu. Fie legile de compoziție 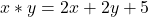 și
și 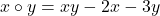 pe mulțimea numerelor reale. Sunt comutative?
pe mulțimea numerelor reale. Sunt comutative?
Rezolvare: Deoarece 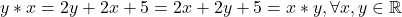 rezultă că legea
rezultă că legea  este comutativă.
este comutativă.
Pentru a doua lege, avem de exemplu 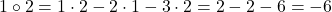 și
și 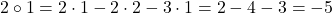 , deci
, deci 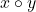 și
și 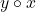 nu au mereu aceeași valoare.
nu au mereu aceeași valoare.
Asociativitate
Definiție: O lege de compoziție ![]() este asociativă dacă
este asociativă dacă ![]() .
.
Exercițiu. Arătați că legea de compoziție ![]() este asociativă.
este asociativă.
Rezolvare: Vom calcula pe rând ![]() și
și ![]() .
.
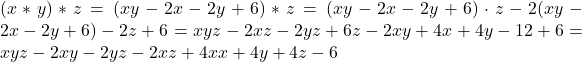 . (1)
. (1)
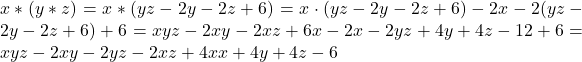 . (2)
. (2)
Din relațiile (1) și (2) rezultă că ![]() și
și ![]() .
.
Element neutru
Definiție: Fie legea de compoziție ![]() . Spunem că legea „*” admite element neutru dacă există
. Spunem că legea „*” admite element neutru dacă există ![]() cu proprietatea că
cu proprietatea că ![]() . În acest caz,
. În acest caz, ![]() se numește element neutru pentru legea de compoziție „*” și este unic.
se numește element neutru pentru legea de compoziție „*” și este unic.
Exercițiu. Determinați elementul neutru al legii de compoziție: ![]() .
.
Rezolvare: ![]() este element neutru al legii de compoziție „*” dacă verifică relația
este element neutru al legii de compoziție „*” dacă verifică relația ![]() . Avem că
. Avem că ![]() , deci este adevărat și pentru
, deci este adevărat și pentru ![]() .
.
Rezolvăm ecuația ![]() și obținem
și obținem ![]() . Pentru ca ecuația anterioară să fie verificată
. Pentru ca ecuația anterioară să fie verificată ![]() rezultă că
rezultă că ![]() este elementul neutru căutat.
este elementul neutru căutat.
Element simetrizabil. Simetricul unui element
Definiție: Fie legea de compoziție ![]() care admite elementul neutru
care admite elementul neutru ![]() . Spunem că elementul
. Spunem că elementul ![]() este simetrizabil în raport cu legea de compoziție „*” dacă există elementul
este simetrizabil în raport cu legea de compoziție „*” dacă există elementul ![]() cu proprietatea că
cu proprietatea că ![]() . În acest caz,
. În acest caz, ![]() se numește simetricul elementului
se numește simetricul elementului ![]() în raport cu legea de compoziție „*”.
în raport cu legea de compoziție „*”.
Exercițiu. Aflați elementele simetrizabile ale legii de compoziție ![]() și
și ![]() .
.
Rezolvare: Mai întâi calculăm elementul neutru al celor două legi. Fie ![]() astfel încât
astfel încât ![]() . Legea „*” este comutativă, deci
. Legea „*” este comutativă, deci ![]() . Din
. Din ![]()
![]() care se verifică pentru orice
care se verifică pentru orice ![]() real dacă
real dacă ![]() . La fel obținem elementul neutru
. La fel obținem elementul neutru ![]() și pentru legea „
și pentru legea „![]() „.
„.
Fie ![]() cu proprietatea că
cu proprietatea că ![]() . Avem că
. Avem că ![]() .
.
Din ![]()
![]() . Așadar, elementele simetrizabile ale legii de compoziție „*” sunt cele din mulțimea
. Așadar, elementele simetrizabile ale legii de compoziție „*” sunt cele din mulțimea ![]() .
.
Pentru legea ![]() avem de rezolvat aceeași ecuație
avem de rezolvat aceeași ecuație ![]() , dar trebuie să punem condiția
, dar trebuie să punem condiția ![]() . Putem scrie
. Putem scrie ![]() care este număr întreg pentru
care este număr întreg pentru ![]() , acestea fiind elementele simetrizabile ale legii de compoziție „
, acestea fiind elementele simetrizabile ale legii de compoziție „![]() „.
„.
Utilizarea legi de compoziție în viața de zi cu zi
Legile de compoziție matematice sunt principii fundamentale care stau la baza structurării și organizării datelor și elementelor în diverse domenii. De la afaceri și tehnologie până la știință și design, aceste legi oferă un cadru logic și coerent pentru a face conexiuni și a realiza analize relevante. Acest articol explorează modul în care legile de compoziție matematice sunt folosite în viața de zi cu zi.
1. Afaceri și Analize Economice: În lumea afacerilor, legile de compoziție matematice sunt esențiale pentru analizele economice. Aceste legi ghidează calculele de profit și pierdere, analizele de tendințe și estimările financiare. Prin aplicarea acestor legi, deciziile de investiții și strategiile de creștere pot fi fundamentate pe date precise și extrapolări corecte.
2. Tehnologie și Dezvoltare Software: În domeniul tehnologiei, legile de compoziție matematice sunt aplicate în dezvoltarea software-urilor complexe. De la algoritmi de criptare la procesarea datelor, aceste legi asigură funcționalitatea corectă și optimizată a aplicațiilor și platformelor tehnologice.
3. Știință și Analize Statistice: În domeniul științei, legile de compoziție matematice sunt fundamentale pentru analizele statistice. Aceste legi sunt folosite pentru interpretarea datelor experimentale, pentru stabilirea corelațiilor și pentru formularea concluziilor științifice solide.
4. Design Grafic și Vizualizare Creativă: În designul grafic și vizualizarea datelor, legile de compoziție matematice sunt aplicate pentru a crea imagini și grafice atrăgătoare și înțelese ușor. Principiile de proporție, balanță și focalizare ghidează crearea unor materiale vizuale pline de impact.
Concluzie:
Legile de compoziție matematice au o prezență puternică și semnificativă în viața noastră de zi cu zi, având un impact într-o varietate de domenii. De la luarea deciziilor economice informate la dezvoltarea tehnologiei avansate și la crearea de vizualizări atractive, aceste legi furnizează un cadru esențial pentru a ne orienta prin complexitatea lumii moderne. Cunoașterea și aplicarea corectă a acestor legi ne ajută să înțelegem mai profund și să navigăm cu încredere prin provocările și oportunitățile prezentului.

