Cercul
Cercul: În acest material despre cerc sunt prezentate următoarele noțiuni: unghi înscris în cerc, coarde și arce în cerc, tangente dintr-un punct exterior la un cerc, poligoane regulate înscrise într-un cerc, lungimea cercului și aria discului. Noțiunile de bază ale cercului se studiază în clasa a 6-a.

Unghi înscris în cerc, coarde și arce în cerc
Cercul reprezintă totalitatea punctelor egal depărtate de un punct fix, numit centrul cercului.
Distanța de la centrul cercului la orice punct de pe cerc este constantă și se numește rază.
Segmentul care unește două puncte de pe cerc se numește coardă.
Totalitatea punctelor de pe cerc, cuprinse între capetele unei coarde, incluzându-le pe acestea, se numește arc de cerc.
Un unghi înscris în cerc este un unghi care are vârful pe cerc și ale cărui laturi conțin două coarde ale cercului.
Măsura unui unghi înscris este egală cu jumătate din măsura arcului cuprins între laturile acestuia.
Unghiul la centru este un unghi care are vârful în centrul cercului și ale cărui laturi conțin două raze ale cercului.
Măsura unui unghi la centru este egală cu măsura arcului cuprins între laturile acestuia.
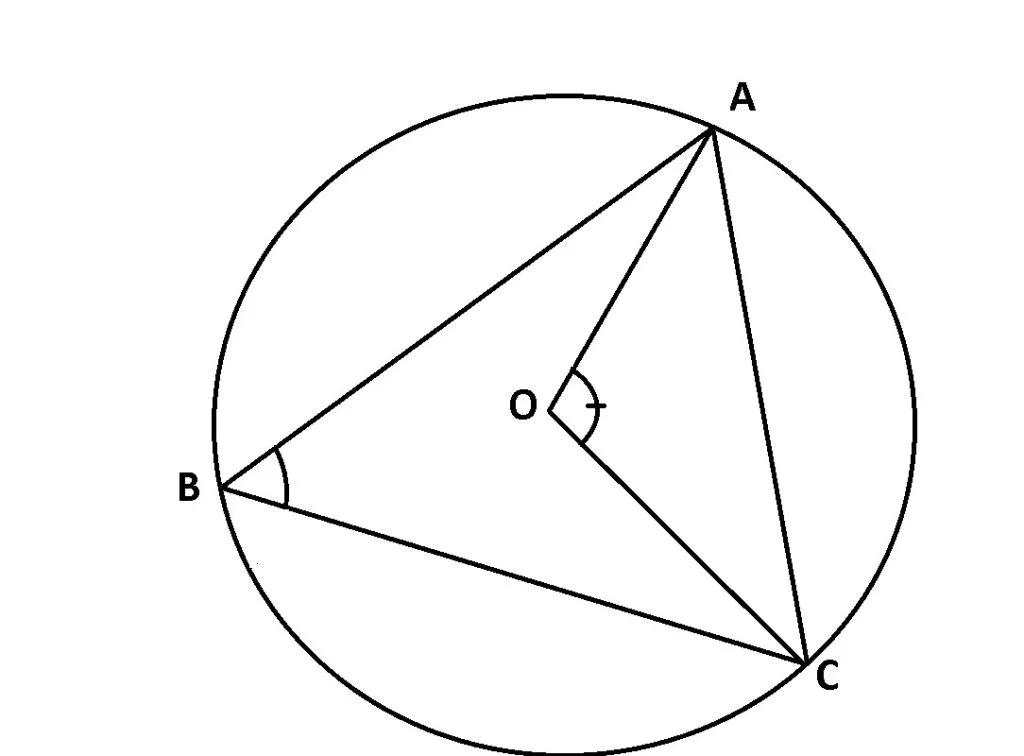
A, B și C sunt trei puncte aflate pe cercul de centru O.
[AC] se numește coardă.
![]() este arc de cerc.
este arc de cerc.
OA este o rază a cercului.
![]() ABC este un unghi înscris în cerc.
ABC este un unghi înscris în cerc.
m![]() ABC =
ABC = ![]()
![]() AOC este un unghi la centru.
AOC este un unghi la centru.
m![]() AOC =
AOC = ![]()
Teorema 1:
În orice cerc, la arce congruente, corespund coarde congruente.
Teorema 2:
În orice cerc, la coarde congruente, corespund arce congruente.
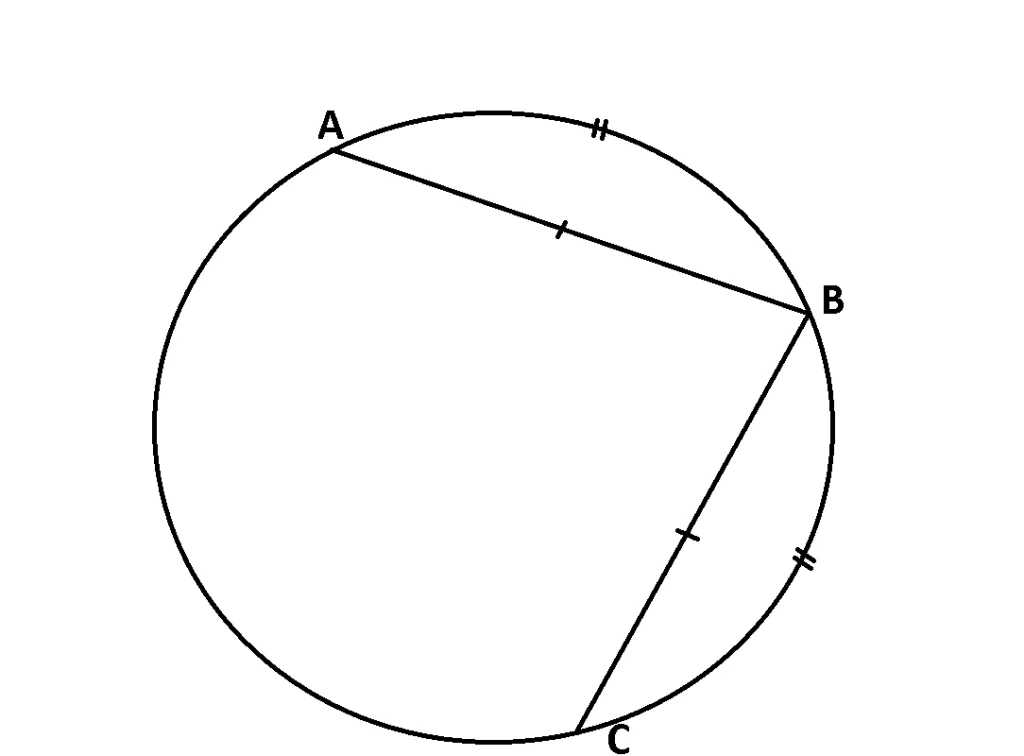
AB, BC coarde:
Dacă ![]() atunci AB = BC.
atunci AB = BC.
Dacă AB = BC, atunci ![]()
Teorema 3:
În oricare cerc, diametrul perpendicular pe o coardă, trece prin mijlocul acesteia și prin mijlocul arcului care este determinat de coardă.
Teorema 4:
Dacă un diametru al unui cerc împarte o coardă sau unul dintre arcele determinate de aceasta în părți congruente, atunci acest diametru este perpendicular pe coardă.
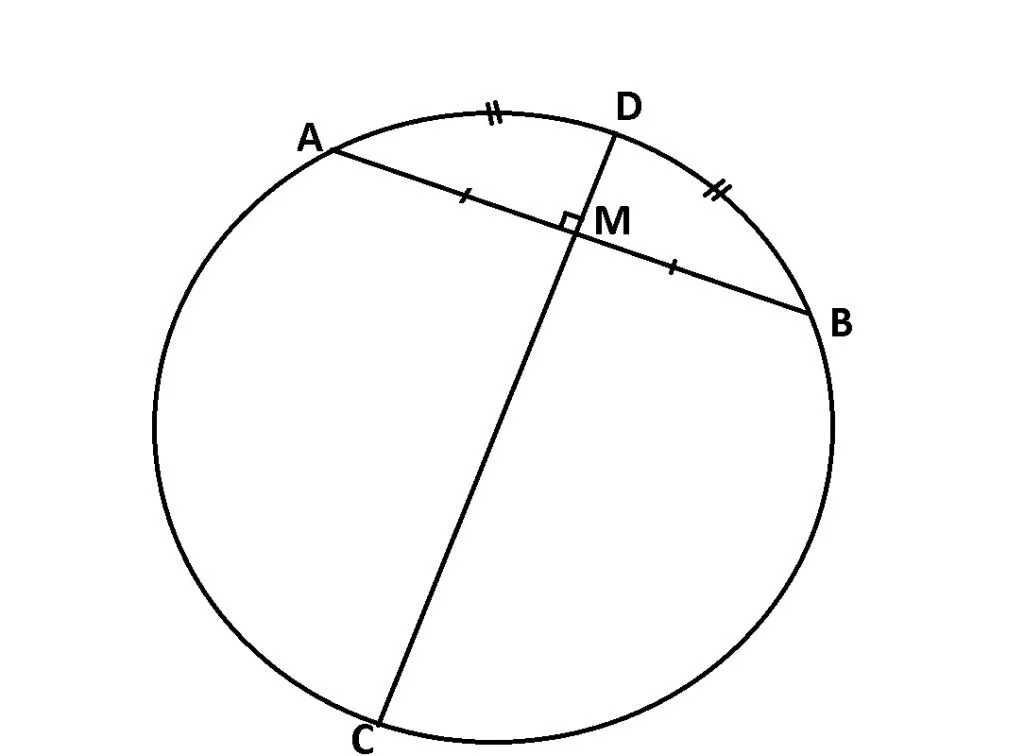
Dacă CD diametru, AB coardă, cu AB ![]() CD, iar AB ∩ CD = {M}, atunci AM = MB și
CD, iar AB ∩ CD = {M}, atunci AM = MB și ![]() .
.
Dacă CD diametru, AB coardă, cu AB ∩ CD = {M}, iar ![]() sau AM = MB, atunci AB
sau AM = MB, atunci AB ![]() CD.
CD.
Teorema 5:
În orice cerc, dacă două coarde sunt egale, atunci ele sunt egal depărtate de centrul cercului.
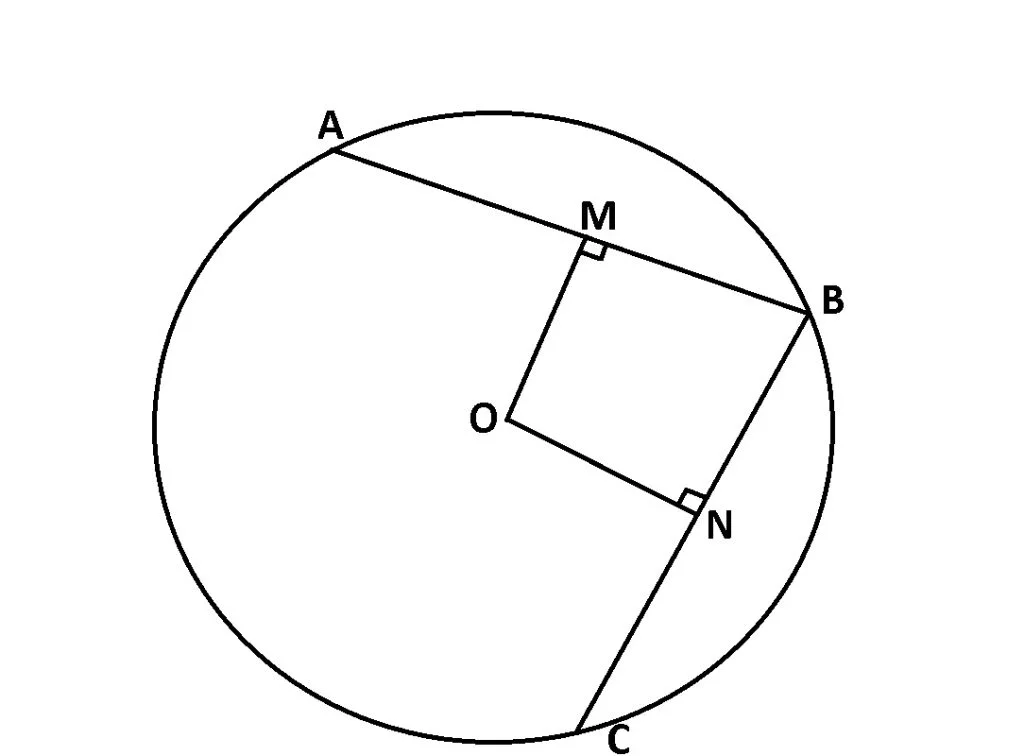
AB, BC coarde:
Dacă AB = BC, atunci d(O, AB) = d(O, BC)
Teorema 6:
În oricare cerc, două coarde paralele determină două arce congruente.

Dacă AB, CD coarde, iar AB || CD, atunci ![]()
Tangente dintr-un punct exterior la un cerc
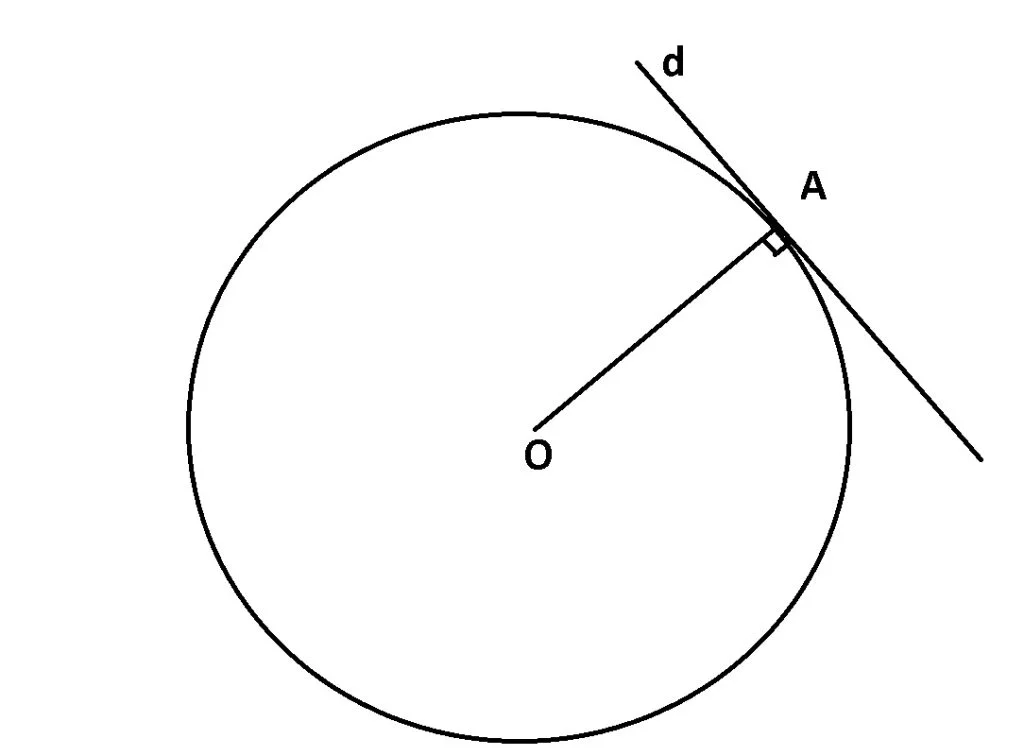
O dreaptă d este tangentă la cercul de centru O și rază R, în punctul A, dacă d ![]() OA.
OA.
Teoremă:
Dintr-un punct exterior unui cerc se pot duce două tangente la cerc. Segmentele determinate de punctul respectiv și punctele de tangență cu cercul sunt congruente.
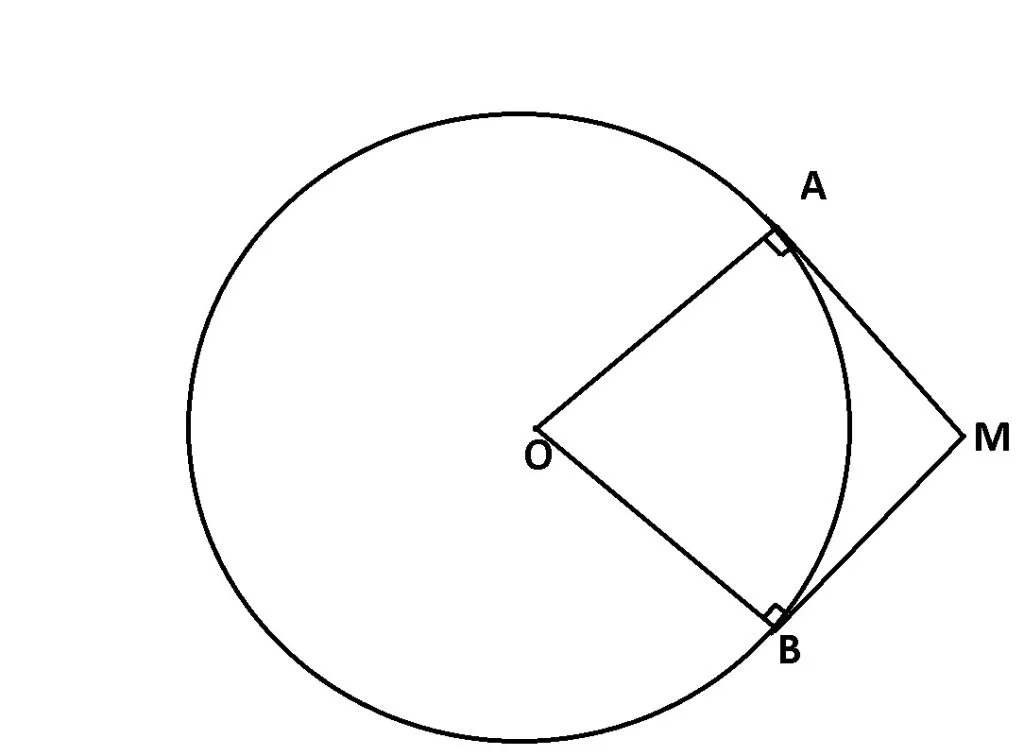
Dacă MA și MB sunt tangente la cerc, unde A și B sunt punctele de tangență cu cercul, atunci MA = MB.
Poligoane regulate înscrise într-un cerc
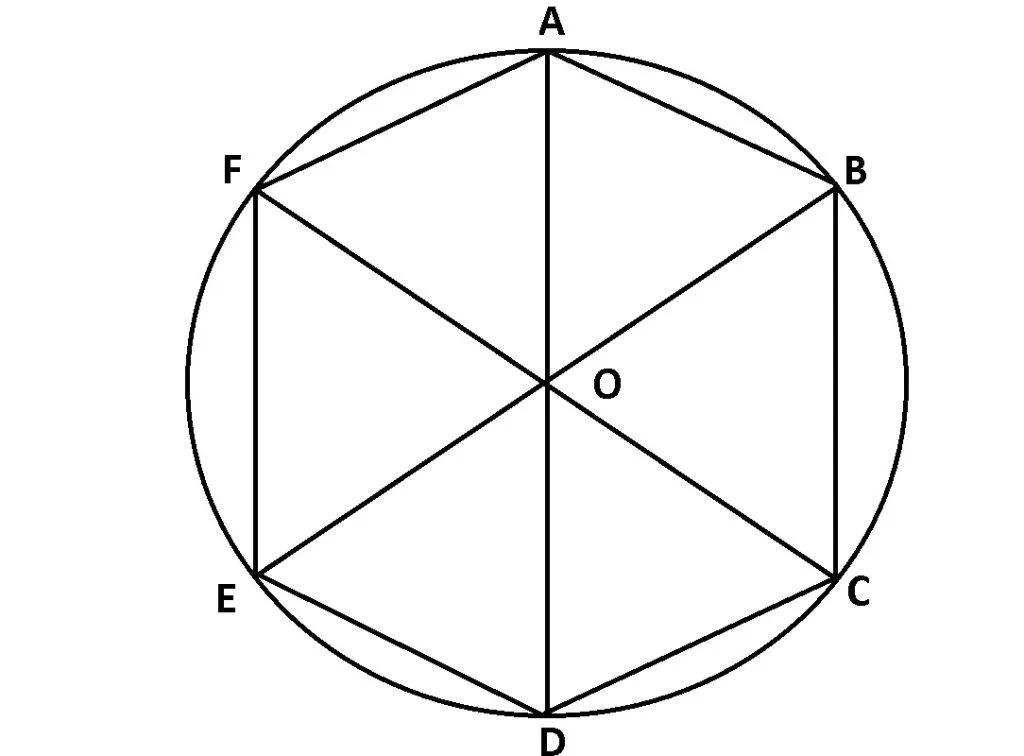
Poligonul regulat este un poligon convex care are toate laturile congruente și toate unghiurile formate de laturi alăturate, congruente.
Cercul care conține toate laturile unui poligon se numește cercul circumscris acestuia.
Poligonul care are toate vârfurile pe un cerc se numește poligon înscris în cerc.
Suma măsurilor unghiurilor unui poligon regulat cu n laturi este (n-2)![]() 180°.
180°.
Unghiul format de două laturi alăturate ale unui poligon regulat are măsura: ![]() °.
°.
Intersecția mediatoarelor laturilor unui poligon regulat reprezintă centrul cercului circumscris acelui poligon.
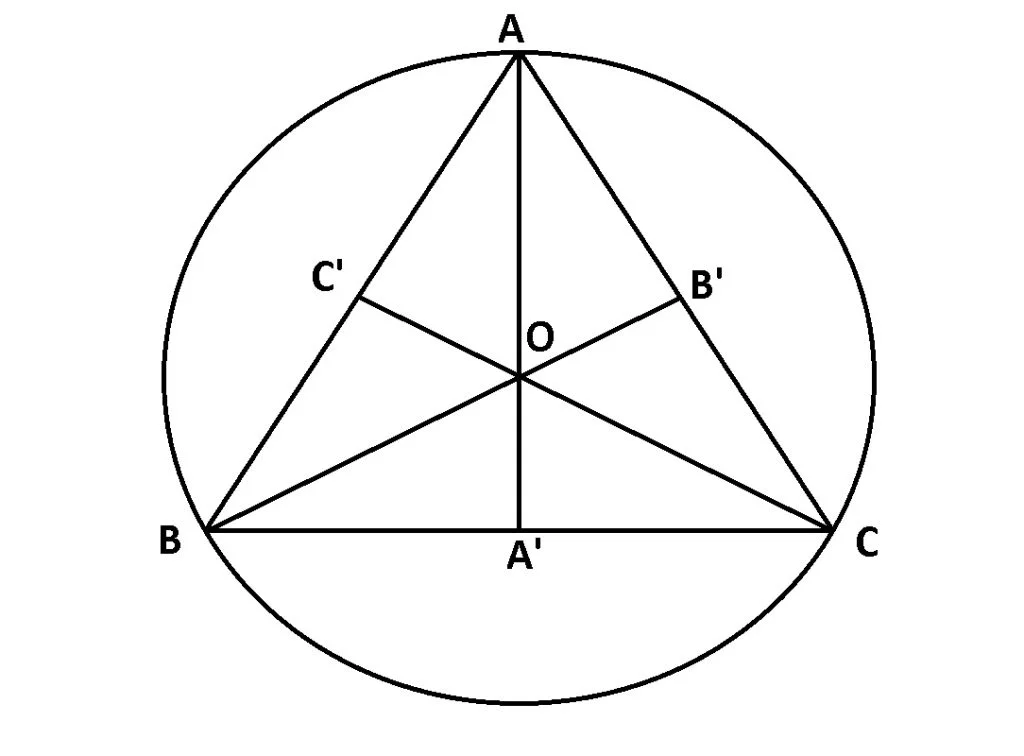
Triunghiul echilateral înscris în cerc
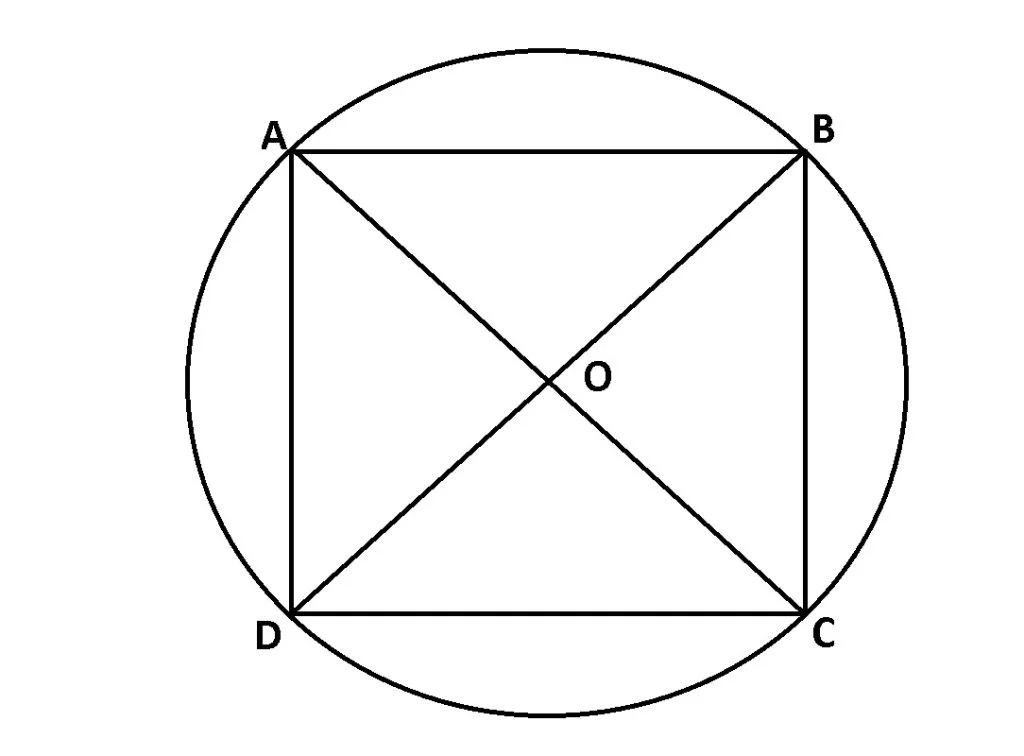
Pătratul înscris în cerc
Hexagonul regulat înscris în cerc
Lungimea cercului și aria discului
Lugimea cercului de centru O si rază R este:
Lcerc=2![]() R
R
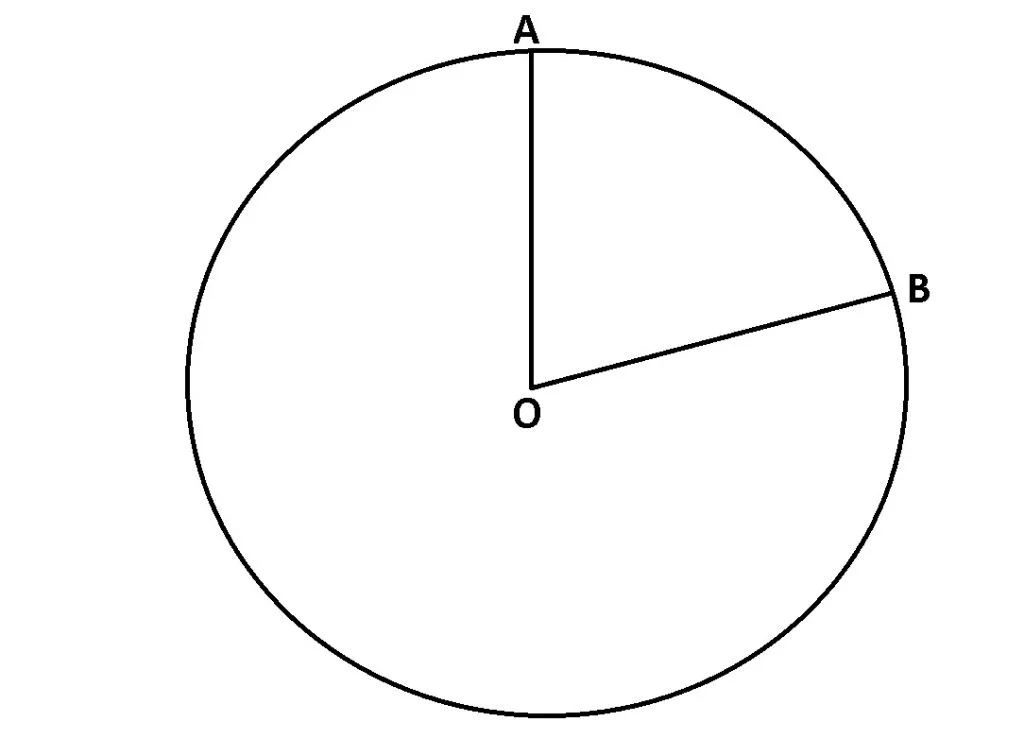
Lungimea arcului de cerc mic ![]() este:
este:
L![]() =
= ![]()
Aria discului aferent cercului de centru O și rază R este:
Acerc = ![]() R2
R2
Aria sectorului de cerc delimitat de razele OA și OB și arcul ![]() este:
este:
Asector cerc = ![]()
Utilizare
Cercul este o formă geometrică de bază, cu numeroase aplicații în diferite domenii.
- În matematică, cercul poate fi utilizat pentru a studia geometria plană și proprietățile sale, cum ar fi raza, diametrul, circumferința și aria. De asemenea, poate fi folosit pentru a rezolva probleme matematice complexe, cum ar fi intersecția dintre două cercuri sau calculul distanței dintre două puncte pe circumferința unui cerc.
- În inginerie, cercul poate fi folosit în proiectarea mecanică, cum ar fi designul roților sau al pieselor rotative. De asemenea, poate fi utilizat în proiectarea sistemelor hidraulice și a sistemelor de transmisie a puterii.
- În artă, cercul poate fi utilizat pentru a crea forme și compoziții, cum ar fi cercurile concentrice în pictură sau formele rotunjite în designul grafic.
În concluzie, cercul are aplicații multiple în matematică, inginerie, artă și alte domenii.

