Radicalul unui număr real 📚

Radicalul unui număr real

Acest material cuprinde următoarele noțiuni: Radicalul unui număr real, proprietăți, definiție, utilizarea în viața reală și se învață în clasa a 10a.

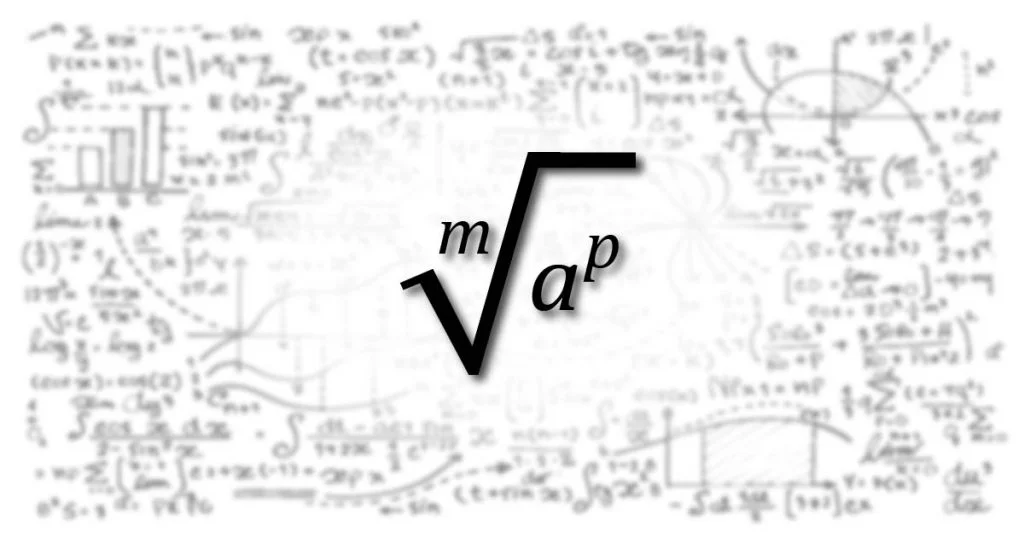
Definiții radicalul unui număr real:

1). Fie numerele $a\geq0, n\in\mathbb{N}, n\geq2, n$ par. Atunci există și este unic un număr real pozitix $x$ astfel încât $x^n=a$ . Acest număr se numește radicalul de ordin $n$ al numărului $a$ și se notează $\sqrt[n]{a}$ .

$x^n=a \Rightarrow x=\sqrt[n]{a}, \forall a\geq0, n\in\mathbb{N}, n\geq2, n$ par, $x\geq0$ .

Ex. $x^6=11$ și $x>0\Rightarrow x=\sqrt[6]{11}; \ \ \ \ x^4=16$ și $x>0\Rightarrow x=\sqrt[4]{16}=2$ .

Observație: Pentru $n=2$ avem rădăcina pătrată a numărului $a$ , care se notează $\sqrt{a}$ .

2). Fie numerele $a\in\mathbb{R}, n\in\mathbb{N}, n\geq2, n$ impar. Atunci există și este unic un număr real pozitix $x$ astfel încât $x^n=a$ . Acest număr se numește radicalul de ordin $n$ al numărului $a$ și se notează $\sqrt[n]{a}$ .

$x^n=a \Rightarrow x=\sqrt[n]{a}, \forall a\in\mathbb{R}, n\in\mathbb{N}, n\geq2, n$ impar.

Ex. $x^5=3\Rightarrow x=\sqrt[5]{3}; \ \ \ \ x^3=-27\Rightarrow x=\sqrt[3]{-27}=-3$ .

Proprietăți ale radicalilor de ordin par

Pentru formulele următoare consideram $n\in\mathbb{N}, n\geq2, n$ par.

1). $(\sqrt[n]{a})^n=a, \forall a\geq0$

Ex. $(\sqrt[8]{5})^8=5$ .

2). $\sqrt[n]{a^n}=|a|, \forall a\in\mathbb{R}$

Ex. $\sqrt[10]{x^{10}}=|x|; \ \ \sqrt[4]{(-2)^4}=|-2|=2$ .

3). $\sqrt[n]{a}\cdot\sqrt[n]{b}=\sqrt[n]{ab}, \forall a\geq0, b\geq0$

Ex. $\sqrt[6]{2}\cdot \sqrt[6]{32}=\sqrt[6]{64}=2$ .

4). $\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}, \forall a\geq0, b>0$

Ex. $\frac{\sqrt[6]{10}}{\sqrt[6]{2}}=\sqrt[6]{5}$ .

5). $\sqrt[n]{a}=a^{\frac{1}{n}}, \forall a\geq0$

Ex. $\sqrt[10]{3}=3^{\frac{1}{10}}$ .

6). $\sqrt[n]{a^m}=a^{\frac{m}{n}}, \forall a\geq0, m\in\mathbb{Z}$

Ex. $\sqrt[10]{3^6}=3^{\frac{6}{10}}=3^{\frac{3}{5}}$ .

7). $(\sqrt[n]{a})^m=\sqrt[n]{a^m}, \forall a\geq0, m\in\mathbb{Z}$

Ex. $(\sqrt[10]{3})^6=\sqrt[10]{3^6}$ .

8). $\sqrt[n]{\sqrt[m]{a}}=\sqrt[n\cdot m]{a}, \forall a\geq0, m\in\matbbb{N}, m\geq 2$ .

Ex. $\sqrt{\sqrt[11]{10}}=\sqrt[22]{10}$ .

9). pentru $0\leq a<b\Rightarrow \sqrt[n]{a}<\sqrt[n]{b}$ .

Ex. $\sqrt[4]{5}<\sqrt[4]{11}$ .

10). $\sqrt[n]{a^n\cdot b}=|a|\sqrt[n]{b}, \forall a\in\mathbb{R}, b\geq 0$ (scoaterea factorilor de sub radical)

Ex. $\sqrt[4]{48}=\sqrt[4]{2^4\cdot 3}=2\sqrt[4]{3}$ .

Proprietăți ale radicalilor de ordin impar

Pentru formulele următoare consideram $n\in\mathbb{N}, n\geq2, n$ impar.

1). $(\sqrt[n]{a})^n=a, \forall a\in\mathbb{R}$

Ex. $(\sqrt[7]{-10})^7=-10$ .

2). $\sqrt[n]{a^n}=a, \forall a\in\mathbb{R}$

Ex. $\sqrt[3]{x^3}=x; \ \ \sqrt[9]{(-2)^9}=-2$ .

3). $\sqrt[n]{a}\cdot\sqrt[n]{b}=\sqrt[n]{ab}, \forall a, b\in\mathbb{R}$

Ex. $\sqrt[3]{9}\cdot \sqrt[3]{3}=\sqrt[3]{27}=3$ .

4). $\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}, \forall a, b\in\mathbb{R}, b\neq0$

Ex. $\frac{\sqrt[3]{16}}{\sqrt[3]{2}}=\sqrt[3]{8}=2$ .

5). $\sqrt[n]{a}=a^{\frac{1}{n}}, \forall a\in\mathbb{R}$

Ex. $\sqrt[7]{-3}=(-3)^{\frac{1}{7}}$ .

6). $\sqrt[n]{a^m}=a^{\frac{m}{n}}, \forall a\in\mathbb{R}, m\in\mathbb{Z}$

Ex. $\sqrt[7]{(-3)^{21}}=(-3)^{\frac{21}{7}}=(-3)^3=-27$ .

7). $(\sqrt[n]{a})^m=\sqrt[n]{a^m}, \forall a\in\mathbb{R}, m\in\mathbb{Z}$

Ex. $(\sqrt[5]{8})^{-2}=\sqrt[5]{8^{-2}}=\sqrt[5]{\frac{1}{64}}=\frac{1}{2\sqrt[5]{2}}$ .

8). $\sqrt[n]{\sqrt[m]{a}}=\sqrt[n\cdot m]{a}, \forall a\in\mathbb{R}, m\in\matbbb{N}, m\geq 2$ .

Ex. $\sqrt[3]{\sqrt[5]{2}}=\sqrt[15]{2}$ .

9). pentru $a<b\Rightarrow \sqrt[n]{a}<\sqrt[n]{b}$ .

Ex. $\sqrt[9]{-1}<\sqrt[9]{5}$ .

10). $\sqrt[n]{a^n\cdot b}=a\sqrt[n]{b}, \forall a, b\in\mathbb{R}$ (scoaterea factorilor de sub radical)

Ex. $\sqrt[3]{81}=\sqrt[3]{3^3\cdot 3}=3\sqrt[3]{3}$ .

Reținem! Radicalii de ordin par sunt numere pozitive și sunt definiți pe numere pozitive, iar radicalii de ordin impar sunt numere reale (pozitive sau negative) și sunt definiți pe numere reale.

Raționalizarea fracțiilor

1). Pentru fracțiile care au la numitor radicali de forma $\sqrt[n]{a}$ (cu $a\geq 0$ și $n$ par sau $a\in\mathbb{R}$ și $n$ impar) se amplifică fracția cu $\sqrt[n]{a^{n-1}}$ .

Ex. $\frac{1}{\sqrt[4]{2}}=\frac{\sqrt[4]{2^3}}{\sqrt[4]{2^4}}=\frac{\sqrt[4]{8}}{2}$ . (am aplificat cu $\sqrt[4]{2^3}$ )

$\frac{5}{2\sqrt[3]{10}}=\frac{5\sqrt[3]{10^2}}{2\sqrt[3]{10^3}}=\frac{5\sqrt[3]{100}}{20}=\frac{\sqrt[3]{100}}{4}$ . (am aplificat cu $\sqrt[3]{10^2}$ )

2). Pentru fracțiile care au la numitor numere de forma $a+b\sqrt{m}$ , $a\sqrt{m}+b$ sau $a\sqrt{m}+b\sqrt{n}$ ( $m,n\geq0$ , $a,b\in\mathbb{Q}$ ) se amplifică fracția cu conjugatul numitorului.

Ex. $\frac{2}{\sqrt{5}-\sqrt{3}}=\frac{2(\sqrt{5}+\sqrt{3})}{5-3}=\sqrt{5}+\sqrt{3}$ .

$\frac{1}{3\sqrt{2}+2\sqrt{3}}=\frac{3\sqrt{2}+2\sqrt{3}}{18-12}=\frac{3\sqrt{2}+2\sqrt{3}}{6}$ .

Pentru următorul caz avem nevoie de două formule de calcul prescurtat:

$x^3+y^3=(x+y)(x^2-xy+y^2)$ (1) și $x^3-y^3=(x-y)(x^2+xy+y^2)$ (2).

3). Pentru fracțiile care au la numitor numere de forma $a\sqrt[3]{b} \pm c\sqrt[3]{d}$ sau $a^2\sqrt[3]{b^2} \pm ac\sqrt[3]{bd}+c^2\sqrt[3]{d^2}$ ( $a,b,c,d\in\mathbb{R}$ ) se amplifică fracția cu conjugatul numitorului, reprezentând paranteza lipsă din formulele de calcul prescurtat de mai sus.

Ex. $\frac{1}{\sqrt[3]{4}+2}=\frac{(\sqrt[3]{4})^2-2\cdot\sqrt[3]{4}+2^2}{(\sqrt[3]{4})^3+2^3}=\frac{\sqrt[3]{16}-2\sqrt[3]{4}+4}{4+8}$ (am folosit formula de calcul prescurtat (1))

$\frac{2}{\sqrt[3]{9}+\sqrt[3]{6}+\sqrt[3]{4}}=\frac{2}{\sqrt[3]{3^2}+\sqrt[3]{3\cdot 2}+\sqrt[3]{2^2}}=\frac{2(\sqrt[3]{3}-\sqrt[3]{2})}{\sqrt[3]{3^3}-\sqrt[3]{2^3}}=\frac{2(\sqrt[3]{3}-\sqrt[3]{2})}{3-2}=2(\sqrt[3]{3}-\sqrt[3]{2})$ (am folosit formula de calcul prescurtat (2))

Utilizarea în viața de zi cu zi: Radicalul unui număr real

Radicalul unui număr real este un concept matematic complex cu aplicații semnificative în contextul vieții de zi cu zi. Deși acest termen poate părea abstract, radicalul joacă un rol esențial într-o serie de domenii, de la construcții și finanțe personale până la tehnologie și sănătate. În acest articol, vom explora diverse moduri în care radicalul unui număr real este folosit în aplicații practice și cum influențează diferite aspecte ale vieții moderne.

Constructii și Inginerie

Radicalul unui număr real este folosit în calculul lungimilor, ariilor și volumelor în construcții și inginerie. În proiectarea clădirilor sau a infrastructurii, cunoașterea radicalului contribuie la determinarea mărimii exacte a materialelor necesare, asigurând eficiența și precizia în construcții.

Tehnologie și Calculul Științific

În era tehnologiei avansate, radicalul unui număr real este utilizat în domeniul calculului științific. Algoritmi complecși, cum ar fi cei din domeniul criptografiei sau al tehnologiilor de securitate online, se bazează pe proprietățile radicalilor pentru a asigura confidențialitatea și autentificarea datelor.

Finanțe Personale și Economie

În sfera finanțelor personale, radicalul unui număr real are un impact semnificativ. În calculul ratelor de dobândă sau al evaluării riscurilor financiare, înțelegerea radicalilor ajută indivizii să facă alegeri informate cu privire la investiții, economii și cheltuieli.

Sănătate și Științe Medicale

În domeniul sănătății, radicalul unui număr real este folosit în analizele medicale și în determinarea unor indicatori importanți precum tensiunea arterială sau fluxul sanguin. Aceste informații esențiale sunt obținute prin aplicarea conceptelor matematice, inclusiv a radicalilor.

Concluzie:

Aplicațiile practice ale radicalului unui număr real sunt diversificate și aduc un beneficiu semnificativ vieții noastre zilnice. De la construcții și tehnologie până la finanțe personale și sănătate, înțelegerea acestui concept matematic complex ne permite să luăm decizii informate și să înțelegem mai profund lumea care ne înconjoară. Cu toate că radicalul poate părea abstract, el este cu siguranță o unealtă esențială pentru progresul și dezvoltarea societății moderne.

Dacă îți place platforma noastră, te invit și pe pagina noastră de Facebook și Youtube

Meniu