Punctul

Punctul se reprezintă printr-o bulină sau prin două liniuțe care se intersectează și se notează cu una din literele mari ale alfabetului.

Două puncte pot fi confundate, dacă coincid, sau distincte:

Puncte confundate:

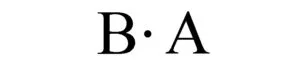
Puncte distincte:

Dreapta

Dreapta este o linie dreaptă, nemărginită, formată dintr-o infinitate de puncte. Dreapta se notează cu o literă mică sau cu două litere mari ale alfabetului.

Mai jos avem dreapta d și dreapta AB sau BA:

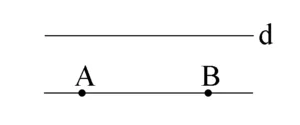
Semidreapta

Semidreapta reprezintă porțiunea unei drepte aflate de aceeași parte a unui punct fixat de pe dreaptă, care este numit originea semidreptei.

Mai jos avem semidreapta AB cu originea în punctul A.

Segmentul de dreaptă

Segmentul de dreaptă reprezintă porțiunea dintr-o dreaptă cuprinsă între două puncte fixate, de pe dreapta respectivă.

Mai jos avem segmentul AB:

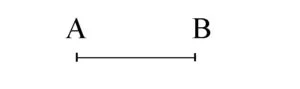
Pozițiile relative ale unui punct față de o dreaptă

Dacă un punct A este situat pe o dreaptă d, spunem că punctul A aparține dreptei d. (A∈d)

Dacă un punct B nu este situat pe o dreaptă d, spunem că punctul B nu aparține dreptei d. (B∉d)

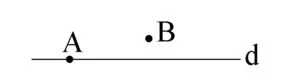
Puncte coliniare

Trei sau mai multe puncte sunt coliniare, dacă există o dreaptă care să conțină acele puncte. (dacă sunt situate pe aceeași dreaptă)

Mai jos, punctele M, N, P sunt coliniare, iar A,B și C nu sunt coliniare.

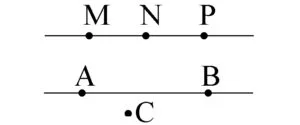
Axioma dreptei

Prin două puncte distincte, trece o dreaptă și numai una.

Pozițiile relative a două drepte

Două drepte care au toate punctele comune (care coincid) se numesc drepte confundate.

Mai jos, d=AB.

Două drepte care au un punct comun (se intersectează într-un punct) se numesc drepte concurente.

Mai jos, a∩b={O}

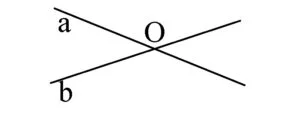
Două drepte care nu au niciun punct comun (situate în același plan) se numesc drepte paralele.

Mai jos, a || b.

Lungimea unui segment. Segmente congruente

Lungimea unui segment reprezintă distanță măsurată între capetele segmentului.

Două segmente sunt congruente dacă au lungimile egale.

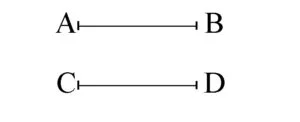
În figura de mai jos, avem două segmente congruente AB și CD.

AB = CD ⇔ AB≡CD.

Mijlocul unui segment

Mijlocul unui segment este un punct unic aflat pe un segment de dreaptă, care formează două segmente congruente cu capetele segmentului.

În figura de mai jos M este mijlocul segmentului AB.

M = mijlocul lui AB. Avem AM = MB = .

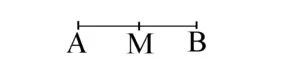
Simetricul unui punct față de alt punct

Simetricul unui punct A față de un punct M este un punct B, cu proprietatea că M este mijlocul lui AB.

Dacă B este simetricul lui A față de M, atunci A este simetricul lui B față de M, iar A și B sunt simetrice față de M.

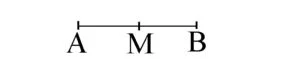
Unghiul

Unghiul este figura geometrică determinată de două semidrepte cu aceeași origine.

În figura de mai jos avem unghiul AOB (∠AOB) sau unghiul O (∠O).

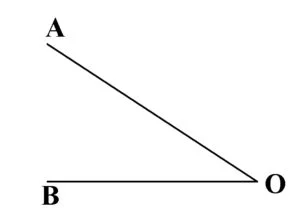
O este vârful unghiului.

Semidreptele OA și OB se numesc laturile unghiului.

Când notăm unghiul cu trei litere, vârful unghiului este litera din mijloc.

Măsura unui unghi

Unitatea de măsură pentru măsurarea unghiurilor, cea mai utilizată, este gradul sexagesimal.

Un grad are 60 de minute.

1° = 60′

Instrumentul cu ajutorul căruia măsurăm un unghi se numește raportor.

Unghiuri congruente

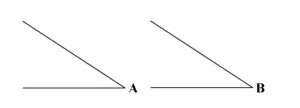
Două unghiuri sunt congruente dacă măsurilor lor sunt egale.

m∠A = m∠B ⇔ ∠A≡∠B

Clasificarea unghiurilor

Unghiul ascuțit este unghiul cu măsura cuprinsă între 0° și 90°.

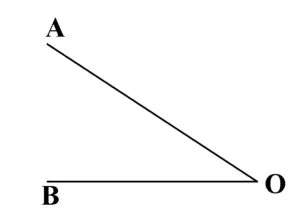
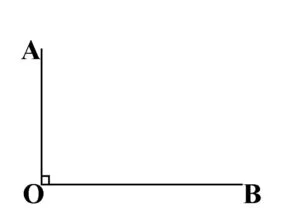
Unghiul drept este unghiul care are fix 90°.

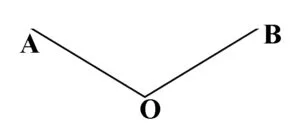
Unghiul obtuz este unghiul care are măsura cuprinsă între 90° și 180°.

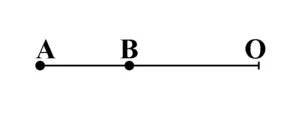
Unghiul nul este unghiul cu măsura de 0°.

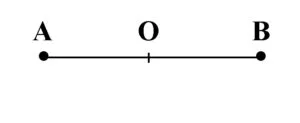
Unghiul alungit este unghiul cu măsura de 180°.

Figuri congruente. Axă de simetrie

În general, două figuri geometrice sunt congruente dacă, prin suprapunere, coincid.

Exemple de figuri congruente:

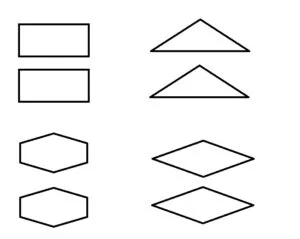
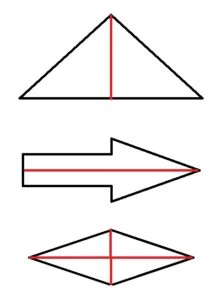
Dacă putem îndoi o figură geometrică de-a lungul unei drepte, astfel încât cele două părți formate să coincidă prin suprapunere. atunci figura geometrică este simetrică. Dreapta după care s-a realizat îndoirea se numește axă de simetrie.

O figura simetrică poate admite axă de simetrie orizontală, axă de simetrie verticală sau mai multe axe de simetrie.

Aplicabilitate

În cadrul clasei a 5-a, copiii sunt introduși în lumea geometriei prin intermediul capitolului Elemente de geometrie. Acest capitol acoperă aspecte precum punct, dreaptă, semidreaptă, segment de dreaptă, pozițiile relative ale unui punct față de o dreaptă, puncte coliniare, axioma dreptei, pozițiile relative a două drepte, lungimea unui segment, segmente congruente, mijlocul unui segment, simetricul unui punct față de un punct, unghiul și elementele unui unghi, măsura unui unghi, unghiuri congruente, clasificarea unghiurilor, figuri congruente, axa de simetrie, oferind elevilor instrumentele de bază necesare pentru a înțelege principiile geometrice.

În plus, studiul geometriei are o aplicabilitate semnificativă în viața reală. Aceasta poate fi folosită în diverse domenii, precum arhitectură, construcții, design grafic, inginerie și multe altele.

Construcții

Un exemplu concret este utilizarea principiilor geometrice în construcția clădirilor. În acest caz, geometria este folosită pentru a calcula dimensiunile și ariile diferitelor părți ale clădirii, precum pereții, ferestrele și ușile. De asemenea, geometria este folosită pentru a crea design-uri precise ale clădirilor, astfel încât acestea să fie sigure și funcționale.

Grafică

În domeniul designului grafic, geometria este folosită pentru a crea forme și modele precise, care pot fi utilizate în diverse proiecte, cum ar fi logo-uri, afișe sau site-uri web. Prin urmare, studiul geometriei poate fi util și pentru acei copii care vor să urmeze o carieră în domeniul designului.

În concluzie, capitolul Elemente de geometrie din clasa a 5-a poate fi considerat un punct de pornire important pentru dezvoltarea unui interes și a unei pasiuni pentru geometrie. Prin înțelegerea principiilor geometrice de bază și aplicarea lor în diverse domenii, elevii pot înțelege importanța geometriei și pot dezvolta abilitățile necesare pentru a folosi această disciplină în viața reală.