Bisectoarea unui unghi a triunghiului reprezintă semidreapta din interiorul unghiului cu originea în vârful acestuia și care formeaza cu laturile acestuia două unghiuri congruente.

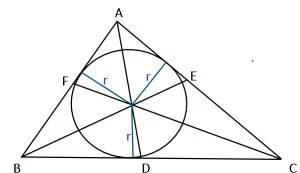
În ΔABC, dacă:

AD = bisectoarea ∢A, atunci m∢BAD = m∢DAC = 
BE = bisectoarea ∢B, atunci m∢ABE = m∢EBC = 
CF = bisectoarea ∢C, atunci m∢ACF = m∢FCB = 

Centrul cercului înscris în triunghi

Punctul de intersecție a bisectoarelor unui triunghi se numește centrul cercului înscris în triunghi.

AD ∩ BE ∩ CF ={I}. I = centrul cercului înscris în triunghi.

Distanțele de la centrul cercului înscris în triunghi și laturile triunghiului sunt egale, fiecare reprezentând raze ale cercului înscris în triunghi.

d(I,AB)=d(I,BC)=d(I,CA)=r (raza cercului înscris în triunghi).

Mediatoarea

Mediatoarea unui segment este dreapta perpendiculară pe segmentul respectiv, care trece prin mijlocul acestuia.

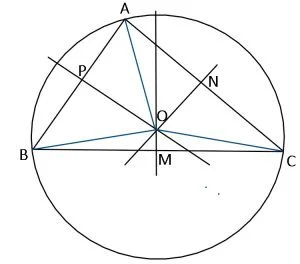
În ΔABC, dacă:

M=mijlocul lui AB și MO Ʇ AB, atunci MO=mediatoarea lui AB
N=mijlocul lui BC și NO Ʇ BC, atunci NO = mediatoarea lui BC
P=mijlocul lui CA și PO Ʇ C, atunci PO = mediatoarea lui CA

Centrul cercului circumscris triunghiului

Punctul de intersecție a mediatoarelor unui triunghi se numește cenmtrul cercului circumscris triunghiului.

MO ∩ NO ∩ PO ={O}. O = centrul cercului circumscris triunghiului.

Distanțele de la centrul cercului circumscris triunghiului la vârfurile triun ghiului sunt egale, fiecare reprezentând raze ale cercului circumscris triunghiului.

OA = OB = OC = R (raza cercului circumscris triunghiului)

Mediana

Mediana într-un triunghi reprezintă segmentul care unește un vârf al triunghiului cu mijlocul laturii opuse.

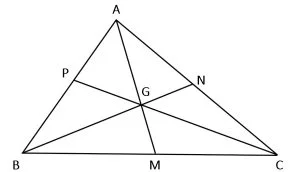
În ΔABC, dacă:

M=mijlocul lui BC, atunci AM = mediana din A
N=mijlocul lui CA, atunci BN = mediana din B
P= mijlocul lui AB, atunci CP = mediana din C

Centrul de greutate al triunghiului

Punctul de intersecție a medianelor într-un triunghi se numește centrul de greutate al triunghiului.

AM ∩ BN ∩ CP ={G}. G = centrul de greutate al triunghiului

Pe fiecare mediană, centrul de greutate se află la o treime de baza triunghiului și două treimi de vârf.

GM =  ∙ AM, GA =  ∙ AM
GN =  ∙ BN, GB =  ∙ BN
GP =  ∙ CP, GC =  ∙ CP

Înălțimea

Înălțimea într-un triunghi este perpendiculara dintr-un vârf al triunghiului pe latura opusă.

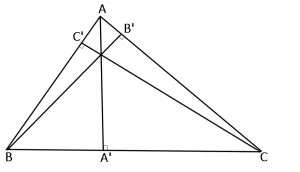
În ΔABC, dacă:

AA’ Ʇ BC (A’ ∈ BC), atunci AA’ = înălțimea din A
BB’ Ʇ AC (B’ ∈ AC), atunci BB’ = înălțimea din B
CC’ Ʇ AB (C’ ∈ AB), atunci CC’ = înălțimea din C

Ortocentrul triunghiului

Punctul de intersecție a înălțimilor unui triunghi se numește ortocentrul triunghiului.

AA’ ∩ BB’ ∩ CC’ ={H}. H = ortocentrul triunghiului.