Mulțimi
Acest material despre mulțimi cuprinde următoarele noțiuni: reprezentarea mulțimilor, apartenența la o mulțime, mulțimi finite și infinite, cardinalul unei mulțimi, relații între mulțimi, operații cu mulțimi.
Mulțimile sunt formate din obiecte (numite elemente) care au o proprietate comună; ele sunt distincte și ordinea lor nu contează; o mulțime de numere se numește mulțime numerică.
Mulțimea vidă = mulțimea care nu are niciun element și se notează cu Ø.

Mulțimea vidă = mulțimea care nu are niciun element și se notează cu Ø.
Reprezentarea mulțimilor
- Prin enumerarea elementelor între acolade A={0,1,2,3,4}
- Prin proprietatea caracteristică A={n/ n natural, n<5}
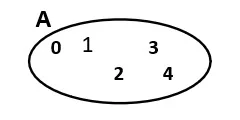
- Prin diagrama Venn-Euler:
Apartenența la o mulțime
Exemplu: Dacă A={0,1,2,3,4}, spunem că:
1 aparține mulțimii A și scriem 1ϵA;
6 nu se află în mulțimea A, deci 6 ∉ A
Mulțimi finite și infinite. Cardinalul unei mulțimi
Mulțime finită=mulțime cu un număr finit de elemente.
Exemplu: A={0,1,2,3,4} are 5 elemente, deci este finită.
Cardinalul unei mulțimi: card A sau |A| = numărul de elemente dintr-o mulțime finită.
Exemplu: A={0,1,2,3,4}
card A=5
Mulțime infinită=mulțime cu număr infinit de elemente.
Exemplu: N(mulțimea numerelor naturale)= {0,1,2,3,4,5 …}
Relații între mulțimi
Mulțimi egale: două mulțimi sunt egale dacă au aceleași elemente;
Exemplu: A={0,1,2,3,4}; B={0,1,2,3,4}, deci A=B
Submulțimea unei mulțimi: A este o submulțime a lui B dacă toate elementele din A sunt și în B.
Exemplu: A={0,1,2,3,4} și B={0,1,2,3,4,5,6}.
A este submulțime a lui B deoarece toate elementele din A, adică 0,1,2,3 și 4 se află și în mulțimea B.
Spunem că A⊂B (A inclus în B) sau B ⊃ A (B include pe A)
Fie mulțimea M={0,1,2,3}. Avem două tipuri de submulțimi:
- Submulțimi improprii (Ø și mulțimea însăși): submulțimile improprii ale lui M sunt si {0,1,2,3}.
- Submulțimi proprii (toate celelalte,dacă există):{0},{1},{2},{3},{0,1},{0,2},{0,3},{1,2},{1,3},{2,3},{0,1,2},{0,1,3},{0,2,3},{1,2,3}.
Operații cu mulțimi
Intersecția a două mulțimi A și B se notează A ∩ B și este formată din elementele comune mulțimilor A și B (care se află și în A și în B).
Exemplu: A={0,1,2,3,4}, B={3,4,5,6,7}.
A ∩ B={3,4}.
Reuniunea a două mulțimi A și B se notează A U B și este formată din toate elementele mulțimilor A și B (care se află în A sau în B)
Exemplu: A={0,1,2,3,4}, B={3,4,5,6,7}.
A U B={0,1,2,3,4,5,6,7}
Diferența a două mulțimi A și B se noteaza A-B sau A\B și este formată din elementele care se află în A și nu se află în B.
Exemplu: A={0,1,2,3,4}, B={3,4,5,6,7}.
A – B={0,1,2}
Aplicabilitate în viața de zi cu zi a Mulțimilor
Capitolul despre Mulțimi în matematică este un pilon fundamental al teoriei matematice care are aplicații extinse într-o varietate de domenii din viața reală. O mulțime este definită ca o colecție de obiecte distincte, iar înțelegerea structurii și relațiilor dintre aceste obiecte este esențială pentru o gamă largă de aplicații practice.
- Un exemplu comun de aplicare a conceptelor de mulțimi este în domeniul populației și demografiei. Să presupunem că suntem interesați de distribuția vârstelor într-o anumită comunitate. Putem utiliza mulțimile pentru a reprezenta diferite categorii de vârstă și pentru a analiza intersectările și diferențele dintre acestea. De asemenea, putem folosi operațiile de reuniune și intersecție pentru a examina subgrupurile de persoane care îndeplinesc anumite criterii, cum ar fi vârsta și genul.
- În domeniul științific, teoria mulțimilor este adesea utilizată pentru a reprezenta și analiza seturi de date. De exemplu, în biologie, putem folosi mulțimile pentru a reprezenta diferite specii de organisme și pentru a analiza relațiile dintre acestea în cadrul unui ecosistem. În chimie, putem utiliza mulțimile pentru a reprezenta diferitele elemente chimice și compuși și pentru a analiza proprietățile și reacțiile acestora.
- În domeniul informaticii, conceptele de mulțimi sunt fundamentale pentru structurile de date și algoritmii utilizate în prelucrarea informațiilor. De exemplu, mulțimile sunt utilizate pentru a reprezenta colecțiile de date în limbaje de programare și pentru a efectua operații precum căutarea, sortarea și eliminarea duplicatelor din seturile de date.
- În economie și afaceri, teoria mulțimilor poate fi utilizată pentru a analiza interacțiunile dintre diferite piețe, consumatori și produse. De exemplu, putem utiliza mulțimile pentru a reprezenta diferitele segmente de piață și pentru a analiza suprapunerile și diferențele dintre acestea. De asemenea, putem folosi mulțimile pentru a reprezenta portofoliile de investiții și pentru a analiza riscurile și randamentele acestora.
În concluzie, teoria mulțimilor din matematică este esențială pentru înțelegerea și analiza relațiilor dintre obiecte și entități într-o varietate de domenii din viața reală. De la populație și demografie la știință și tehnologie, conceptele de mulțimi au aplicații diverse și ubiquitare care ne ajută să înțelegem și să modelăm lumea înconjurătoare.

