Perpendicularitatea
Acest material despre perpendicularitate cuprinde următoarele noțiuni: drepte perpendiculare, distanța de la un punct la o dreaptă, drepte oblice, mediatoarea unui segment, simetria față de o dreaptă. Perpendicularitatea se va studia și în clasa a 8-a unde vor fi predate noțiuni mai complexe.
Drepte perpendiculare
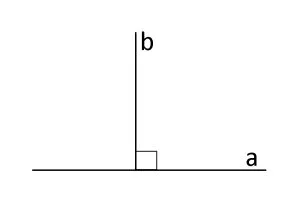
Două drepte sunt perpendiculare dacă formează un unghi drept (de 90°).
Notăm a ⊥ b sau b ⊥ a.
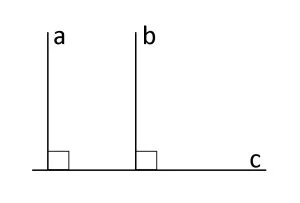
Două drepte distincte perpendiculare pe o a treia dreaptă sunt paralele între ele:
a ⊥ c și b ⊥ c => a || b
Distanță de la un punct la o dreaptă
Distanța de la un punct la o dreptă reprezintă distanța dintre punct și piciorul perpendicularei din acel punct pe acea dreaptă.
d(A,d) = AB, unde B ϵ d, AB ⊥ d
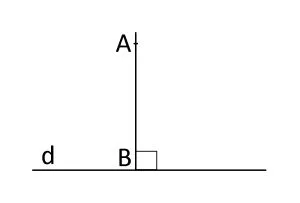
Dintr-un punct dat se poate duce o singură perpendiculară pe o dreaptă dată.
Drepte oblice
Două drepte concurente care nu sunt perpendiculare, sunt oblice una față de cealaltă.
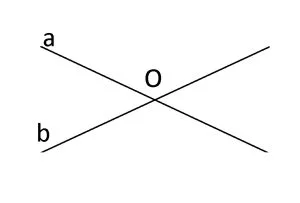
Mediatoarea unui segment
Mediatoarea unui segment este dreapta care trece prin mijlocul segmentului și este perpendiculară pe acesta.
d ⊥ AB și O ϵ d, unde O = mijlocul lui AB => d este mediatoarea lui [AB]
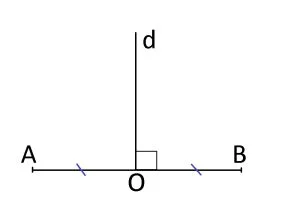
Orice punct de pe mediatoare este egal departat de capetele segmentului:
Daca d este mediatoarea lui [AB], iar M se află pe d, atunci MA = MB.
Simetria față de o dreaptă
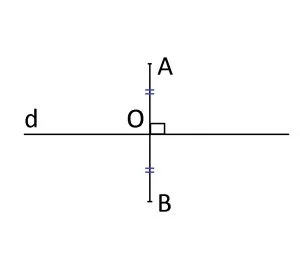
Două puncte A și B sunt simetrice față de o dreptă d, dacă d este mediatoarea segmentului AB.
Dreapta d se numește axă de simetrie.
A = simetricul lui B față de d (A=S![]() B)
B)
B = simetricul lui A față de d (B=S![]() A)
A)
Perpendicularitate: Aplicabilitate
- În arhitectură, perpendicularitatea joacă un rol crucial în proiectarea și construcția clădirilor. De exemplu, pentru a asigura stabilitatea și rezistența unei structuri, pereții verticali ai clădirii trebuie să fie perpendiculari la fundație și la alte elemente structurale. În plus, ușile și ferestrele sunt adesea instalate perpendicular pe pereți pentru a crea un aspect armonios și pentru a asigura o funcționalitate corespunzătoare.
- În industria mașinilor și a fabricației, perpendicularitatea este esențială în asamblarea și reglarea componentelor. De exemplu, în fabricarea pieselor mecanice, suprafețele de referință trebuie să fie perpendiculari pentru a se asigura un montaj corect și o funcționalitate precisă. Utilizarea instrumentelor de măsură precum nivelurile și goniometrele ajută la verificarea și ajustarea perpendicularității în aceste aplicații.
- Perpendicularitatea are, de asemenea, o importanță semnificativă în domeniul optic. În optică, oglinzile și lentilele sunt concepute să creeze imagini clare și nedeformate prin respectarea legii reflexiei și a refracției, care presupun unghiuri de incidentă și refracție perpendiculare pe suprafețele optice. Această corelație dintre perpendicularitateși optică este esențială în designul telescoapelor, microscoapelor și a altor instrumente optice.
În concluzie, perpendicularitatea este un concept geometric cu o mare relevanță în numeroase domenii. Aplicațiile sale se întind de la geometria plană și arhitectură până la inginerie și optică. Înțelegerea și aplicarea corectă a perpendicularității sunt vitale pentru obținerea rezultatelor precise și fiabile în aceste domenii.

