Triunghiul
Triunghiul, acest material cuprinde următoarele noțiuni: noțiuni de bază, suma măsurilor unghiurilor unui triunghi, unghi exterior unui triunghi, clasificarea triunghiurilor în funcție de unghiuri, clasificarea triunghiurilor în funcție de laturi.

Triunghiul – noțiuni de bază
Triunghiul reprezintă figura geometrică formată din reuninea celor trei segmente determinate de trei puncte necoliniare.
În ΔABC, avem:
A,B,C = vârfuri, AB, BC, AC = laturi
∢A (∢BAC), ∢B (∢ABC), ∢C(∢ACB) = unghiurile triunghiului.
Suma măsurilor unghiurilor unui triunghi
Suma măsurilor unghiurilor unui triunghi este 180°:
În ΔABC, avem: m∢A + m∢B + m∢C = 180°
Perimetrul unui triunghi
Perimetrul unui triunghi se determină calculând suma celor trei laturi:
PΔABC = AB+BC+AC
Unghiul exterior unui triunghi
Unghiul exterior unui triunghi este unghiul adiacent și suplementar cu un unghi al triunghiului.
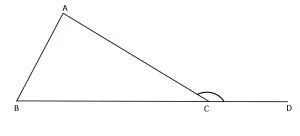
∢ACD = unghiul exterior al lui ∢C => m∢ACD = 180° – m∢C = m∢A + m∢B
Clasificarea triunghiurilor în funcție de unghiuri
În funcție de măsurile unghiurilor, triunghiul se clasifică astfel:
1. Triunghiul ascuțitunghic
Triunghiul ascuțitunghic este triunghiul care are toate unghiurile ascuțite.
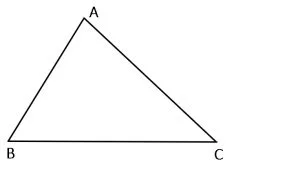
ΔABC ascuțitunghic:
0° < m∢A < 90°
0° < m∢B < 90°
0° < m∢C < 90°
2. Triunghiul dreptunghic
Triunghiul dreptunghic este triunghiul care are un unghi drept.
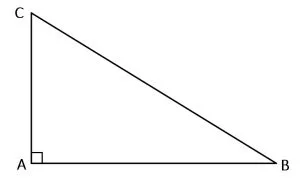
ΔABC dreptunghic:
m∢A = 90°
0° < m∢B < 90°
0° < m∢C < 90°
3. Triunghiul obtuzunghic
Triunghiul obtuzunghic este triunghiul care are un unghi obtuz
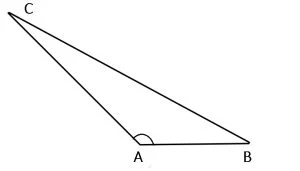
ΔABC obtuzunghic:
90° < m∢A < 180°
0° < m∢B < 90°
0° < m∢C < 90°
Clasificarea triunghiurilor în funcție de laturi
În funcție delaturi, triunghiul se clasifică astfel:
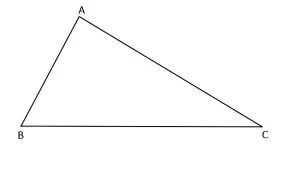
1. Triunghiul oarecare (scalen)
Triunghiul oarecare este triunghiul în care oricare două laturi sunt de lungimi diferite.
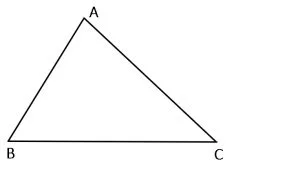
ΔABC oarecare:
AB ≠ BC
BC ≠ CA
CA ≠ AB
2. Triunghiul isoscel
Triunghiul isoscel este triunghiul care are două laturi congruente.
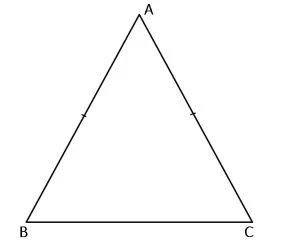
ΔABC isoscel:
AB = AC.
A = vârful triunghiului isoscel. BC = baza triunghiului isoscel.
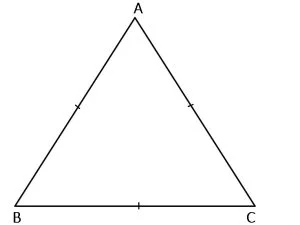
3. Triunghiul echilateral
Triunghiul echilateral este triunghiul cu toate laturile congruente.
ΔABC echilateral:
AB = BC = AC.