Un triunghi care are două laturi congruente se numește triunghi isoscel.

În figura de mai jos, triunghiul ABC este isoscel cu AB≡AC.

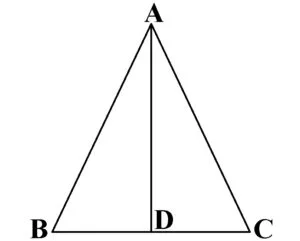
Proprietățile triunghiului isoscel:

• unghiurile de la bază sunt congruente: ∠B ≡ ∠C
• înalțimea dusă din vârful triunghiului, bisectoarea unghiului de la vârf, mediana din vârful triunghiului și mediatoarea corespunzătoare bazei coincid și reprezintă axa de simetrie a triunghiului. Dacă AD este înălțimea din A, atunci este și bisectoarea unghiului A, mediana din A și mediatoarea laturii BC, precum și axa de simetrie a triunghiului ABC.

Cum arătăm că un triunghi este isoscel?

• arătăm că are două laturi congruente, sau:
• arătăm că are două unghiuri congruente, sau:
• arătăm că două linii importante coincid.
•  

Proprietățile triunghiului echilateral

Un triunghi care are toate laturile congruente se numește triunghi echilateral.

În figura de mai jos, triunghiul ABC este echilateral cu AB≡BC≡AC.

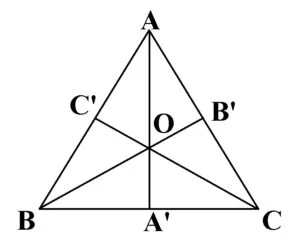
Proprietățile triunghiului echilateral:

• Toate unghiurile triunghiului sunt congruente și au măsura de 60°: ∠A ≡ ∠B ≡ ∠C = 60°.
• înalțimea dusă dintr-un vârf al triunghiului, bisectoarea unghiului de la acel vârf, mediana din același vârful triunghiului și mediatoarea corespunzătoare laturii opuse acelui vârf coincid și reprezintă axa de simetrie a triunghiului: Dacă AA este înălțimea din A, atunci este și bisectoarea unghiului A, mediana din A și mediatoarea laturii BC, precum și ax[ de simetrie a triunghiului ABC.
• centrul de greutate, ortocentrul, centrul cercului înscris în triunghi și centrul cercului circumscris triunghiului coincid.
• Toate cele trei înălțimi ale triunghiului (mediane, bisectoare, mediatoare) sunt congruente: AA’ ≡ BB’≡ CC’, unde AA’ este înalțimea din A, BB’ este înalțimea din B, CC’ este înalțimea din C.

Cum arătăm că un triunghi este echilateral?

• arătăm că are toate laturile congruente, sau:
• arătăm că are toate unghiurile congruente, sau:
• arătăm că are două unghiuri de 60°, sau:
• arătăm că triunghiul este isoscel cu un unghi de 60°, sau:
• arătăm că cele trei înălțimi (bisectoare, mediane, mediatoare) sunt congruente, sau:
• arătăm că două linii importante diferite (bisectoare / înălțimi / mediane / mediatoare) duse din aceleași două vârfuri ale triunghiului coincid, sau:
• două puncte de intersecție ale liniilor importante coincid.

Proprietățile triunghiului dreptunghic

Un triunghi care are un unghi de 90° se numește triunghi dreptunghic.

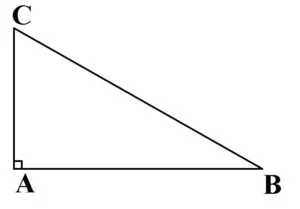
În figura de mai jos, triunghiul ABC este dreptunghic cu unghiul A de 90°.

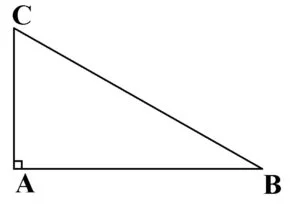
Laturile care formează unghiul de 90° se numesc catete: AB, AC catete.

Latura opusă unghiului de 90° se numește ipotenuză: BC ipotenuză.

Într-un triunghi dreptunghic, unghiurile ascuțite sunt complementare: ∠B + ∠C = 90°. Dacă într-un triunghi, două unghiuri sunt complementare, atunci triunghiul este dreptunghic.

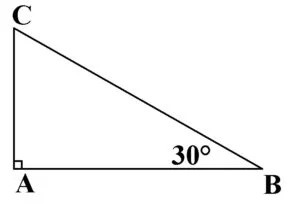
Teorema unghiului de 30°: într-un triunghi dreptunghic, cu un unghi ascuțit de 30°, cateta opusă unghiului de 30° este jumătate din ipotenuză.

În triunghiul ABC, cu ∠A = 90°, dacă ∠B = 30°, atunci AC=

Reciproca: Dacă într-un triunghi dreptunghic, una dintre catete este jumătate din ipotenuză, atunci unghiul care i se opune este de 30°.

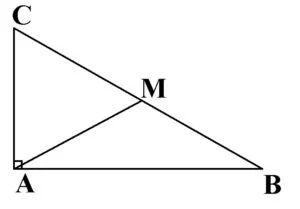
Teorema medianei: Într-un triunghi dreptunghic, mediana care pleacă din vârful unghiului drept este jumătate din ipotenuză.

În triunghiul ABC, cu ∠A = 90°, dacă AM mediană, atunci AM=

Reciproca: Dacă într-un triunghi, o mediană este jumătate din latura care îi corespunde, atunci triunghiul este dreptunghic, unghiul drept fiind cel din vârful căreia s-a dus mediana.

Teorema lui Pitagora: Dacă un triunghi este dreptunghic, atunci pătratul lungimii ipotenuzei este egal cu suma pătratelor lungimilor catetelor.

În triunghiul ABC, cu ∠A = 90°, avem BC2 = AB2 + AC2

Reciproca: Dacă într-un triunghi, pătratul lungimii uneia dintre laturi este egal cu suma pătratelor celorlalte două laturi, atunci triunghiul este dreptunghic, având unghiul drept fiind cel opus primei laturi.

Aplicabilitate

Triunghiurile particulare sunt triunghiuri care au proprietăți speciale și care se întâlnesc adesea în matematică și în viața de zi cu zi.

Aceste triunghiuri particulare au o importanță deosebită în trigonometrie, care este o ramură a matematicii care se ocupă cu relațiile dintre laturile și unghiurile triunghiurilor. Prin utilizarea funcțiilor trigonometrice precum sinus, cosinus și tangenta, putem calcula unghiurile și lungimile laturilor în triunghiurile particulare.

În concluzie, triunghiurile particulare sunt forme geometrice cu proprietăți speciale, care sunt utilizate în diferite domenii, inclusiv în construcții, în navigație sau în calcularea unghiurilor și a distanțelor în trigonometrie. Cunoașterea acestor triunghiuri și a proprietăților lor poate fi foarte utilă pentru a rezolva probleme și pentru a calcula unghiuri și distanțe în diferite situații practice.