Unghiuri opuse la vârf. Unghiuri în jurul unui punct. Unghiuri formate de două drepte paralele cu o secantă.
Acest material cuprinde următoarele noțiuni: unghiuri opuse la vârf, unghiuri în jurul unui punct, drepte paralele, unghiuri formate de două drepte paralele cu o secantă, criterii de paralelism.

Unghiuri opuse la vârf
Unghiurile opuse la vârf sunt unghiuri care au același vârf și laturile unuia sunt în prelungirea laturilor celuilalt (laturile lor sunt perechi de semidrepte opuse).
Unghiurile opuse la vârf sunt congruente.

AC ∩ BD = {O}
![]() (unghiuri opuse la vârf)
(unghiuri opuse la vârf)
![]() (unghiuri opuse la vârf)
(unghiuri opuse la vârf)
Observație:
Perechile de unghiuri alăturale sunt adiacente suplementare:
m(![]() ) + m(
) + m(![]() ) = 180°
) = 180°
m(![]() ) + m(
) + m(![]() ) = 180°
) = 180°
m(![]() ) + m(
) + m(![]() ) = 180°
) = 180°
m(![]() ) + m(
) + m(![]() ) = 180°
) = 180°
Unghiuri în jurul unui punct
Unghiurile în jurul unui punct reprezintă un număr finit de unghiuri cu același vârf, cu interioare disjuncte; orice punct din plan se află pe o latură sau în interiorul unui unghi.
Suma măsurilor în jurul unui punct este de 360°
∢AOB, ∢BOC, ∢COD, ∢DOE și ∢EOA sunt unghiuri în jurul punctului O.
∢AOB + ∢BOC + ∢COD + ∢DOE + ∢EOA = 360°.
Drepte paralele. Unghiuri formate de două drepte paralele și o secantă
Drepte paralele:
Două drepte situate în același plan, care nu au niciun punct comun se numesc drepte paralele.
Două drepte situate în același plan, care au fix un punct comun se numesc drepte concurente.
Două drepte situate în același plan care au cel puțin două puncte comune se numesc drepte confundate.
Axioma lui Euclid: Printr-un punct exterior unei drepte se poate duce o singura dreaptă paralelă și numai una, la dreapta dată.
Unghiuri formate de două drepte paralele intersectate cu o secantă
O dreaptă d care intersectează două drepte distincte a și b în două puncte diferite se numește secantă.
În figura de mai jos sunt reprezentate două drepte paralele a și b, intersectate de o secantă d:
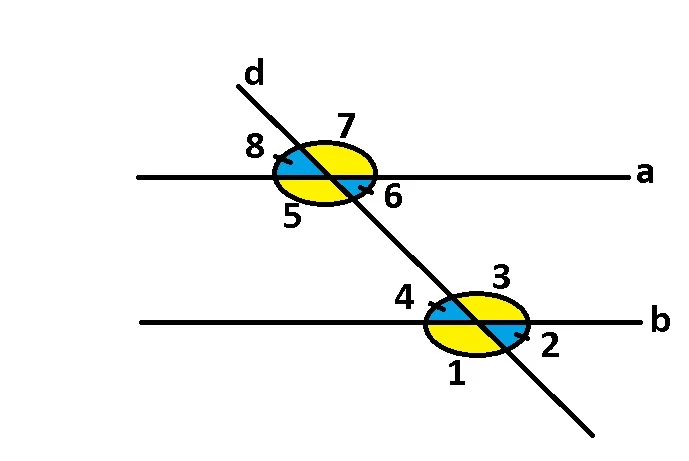
Două drepte paralele intersectate de o secantă formează:
- unghiuri alterne interne congruente:
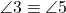 și
și 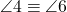
- unghiuri alterne externe congruente:
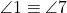 și
și 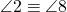
- unghiuri corespondente congruente:
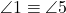 ,
, 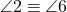 ,
, 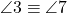 și
și 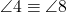
- unghiuri interne, de aceeași parte a secantei, suplementare:
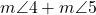 =180° și
=180° și 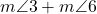 =180°
=180° - unghiuri externe, de aceeași parte a secantei, suplementare:
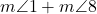 =180° și
=180° și 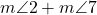 =180°
=180°
Criterii de paralelism:
Teorema unghiurilor alterne interne congruente: dacă două drepte intersectate de o secantă formează o pereche de unghiuri alterne interne congruente, atunci cele două drepte sunt paralele.
Consecințe
- Dacă două drepte intersectate de o secantă formează o pereche de unghiuri alterne externe congruente, atunci cele două drepte sunt paralele.
- Dacă două drepte intersectate de o secantă formează o pereche de unghiuri corespondente congruente, atunci cele două drepte sunt paralele.
- Dacă două drepte intersectate de o secantă formează o pereche de unghiuri interne, de aceeași parte a secantei suplementare, atunci cele două drepte sunt paralele.
- Dacă două drepte intersectate de o secantă formează o pereche de unghiuri externe, de aceeași parte a secantei suplementare, atunci cele două drepte sunt paralele.

