Determinarea elementelor în poligoane regulate

Acest material despre determinarea elementelor în poligoane regulate cuprinde următoarele teme: calculul elementelor în triunghi echilateral, calculul elementelor în pătrat, calculul elementelor în hexagon regulat.

Triunghiul echilateral

Într-un triunghi echilateral, toate laturile sunt congruente, cele trei unghiuri sunt congruente, având fiecare 60°, iar liniile importante coincid și se intersectează în centrul cercului circumscris, care coincide cu ortocentrul, centrul de greutate și centrul cercului înscris.

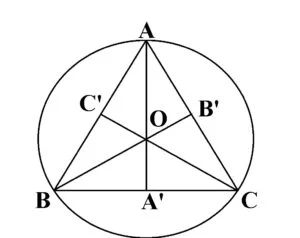
Fie triunghiul ABC echilateral, AA’, BB’, CC’ înălțimi, A’∈BC, B’∈ AC, C’∈AB. (deci AA’, BB’, CC’ mediane, mediatoare și bisectoare).

AB=AC=BC=l (latura triunghiului echilateral)

P_{Δechilateral} = 3l

AA’ = BB’ = CC’ ( h_{Δechilateral})= $\dfrac{l\sqrt{3}}{2}$

A_{Δechilateral} = $\dfrac{l^2\sqrt{3}}{4}$

OA’ = OB’ = OC’ (apotemele triunghiului echilateral) = $\dfrac{l\sqrt{3}}{6}$

OA = OB = OC (razele cercului circumscris) = $\dfrac{l\sqrt{3}}{3}$

Determinarea elementelor în poligoane regulate

Pătratul

Într-un pătrat, laturile sunt congruente, cele patru unghiuri sunt congruente, având fiecare 90°, iar diagonalele au lungimi egale și se înjumătățesc. Intersecția diagonalelor este centrul cercului circumscris.

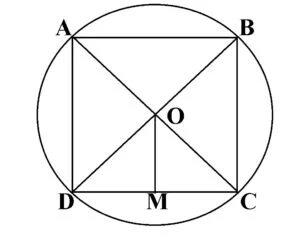
Fie ABCD pătrat, AC și BD diagonale, iar punctul O intersecția diagonalelor.

AB=BC=CD=DA=l (latura pătratului)

P_pătratului = 3l

AC = BD (diagonala pătratului) = l $\sqrt{2}$

A_pătratului = l²

Fie M distanța de la O la CD, atunci OM este apotema pătratului. OM = $\dfrac{l}{2}$

OA = OB =OC = OD (raza cercului circumscris pătratului) = $\dfrac{l\sqrt{2}}{2}$

Hexagonul regulat

Într-un hexagon regulat, laturile sunt congruente, cele patru unghiuri sunt congruente, având fiecare 120°.

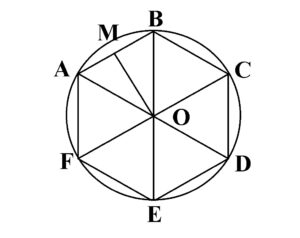
Fie ABCDEF hexagon regulat, cu O centrul cercului circumscris.

AB=BC=CD=DE=EF=FA=l (latura hexagonului regulat)

P_{hexagon regulat} = 6l

A_{hexagon regulat} = $\dfrac{3l^2\sqrt{3}}{2}$

Fie M distanța de la O la AB, atunci OM este apotema hexagonului regulat. OM = $\dfrac{l^2\sqrt{3}}{4}$

OA = OB =OC = OD =OE = OF (raza cercului circumscris hexagonului) = l

Utilizarea calculului elementelor geometrice în viața reală

Geometria joacă un rol important în viața de zi cu zi, iar triunghiurile echilaterale, pătratele și hexagoanele regulate apar frecvent în diverse contexte practice. Iată câteva exemple:

1. Calculul elementelor în triunghi echilateral

Context: Un constructor dorește să amenajeze o grădină sub formă de triunghi echilateral. Latura triunghiului măsoară 6 metri, iar constructorul trebuie să calculeze aria pentru a determina cantitatea de gazon necesar. De asemenea, trebuie să știe înălțimea triunghiului pentru a instala un stâlp central.

Rezolvare:

Formula pentru aria triunghiului echilateral:
$A = \frac{\sqrt{3}}{4} \cdot a^2$
$A = \frac{\sqrt{3}}{4} \cdot 6^2 = \frac{\sqrt{3}}{4} \cdot 36 = 9\sqrt{3} \ \text{m}^2$
Aria grădinii este aproximativ $15.59 \ \text{m}^2$ .
Înălțimea triunghiului:
$h = \frac{\sqrt{3}}{2} \cdot a$
$h = \frac{\sqrt{3}}{2} \cdot 6 = 3\sqrt{3} \ \text{m}$
Înălțimea este aproximativ $5.2 \ \text{m}$ .

2. Calculul elementelor în pătrat

Context: Un artist plastic creează o ramă pătrată din lemn. El știe că latura ramei măsoară 2 metri, iar pentru a adăuga un design simetric, are nevoie să știe diagonala pătratului.

Rezolvare:

Diagonala pătratului:
$d = a\sqrt{2}$
$d = 2\sqrt{2} \ \text{m}$
Diagonala este aproximativ $2.83 \ \text{m}$ .
Aria pătratului (pentru a calcula spațiul pe care îl va ocupa designul):
$A = a^2$
$A = 2^2 = 4 \ \text{m}^2$ .

Astfel, rama ocupă o suprafață de 4 metri pătrați.

3. Calculul elementelor în hexagon regulat

Context: O companie dorește să creeze plăci ceramice sub formă de hexagoane regulate pentru decorul unei podele. Dacă o placă are latura de 10 cm, se calculează aria fiecărei plăci și perimetrul pentru designul marginii.

Rezolvare:

Perimetrul hexagonului:
$P = 6 \cdot a$
$P = 6 \cdot 10 = 60 \ \text{cm}$ .
Aria hexagonului regulat:
$A = \frac{3\sqrt{3}}{2} \cdot a^2$
$A = \frac{3\sqrt{3}}{2} \cdot 10^2 = \frac{3\sqrt{3}}{2} \cdot 100 = 150\sqrt{3} \ \text{cm}^2$
Aria este aproximativ $259.81 \ \text{cm}^2$ .

Concluzie

Astfel de calcule sunt indispensabile în arhitectură, design și construcții. Ele ne ajută să planificăm mai eficient materialele necesare și să proiectăm structuri estetice și funcționale.

Dacă îți place platforma noastră, te invit și pe pagina noastră de Facebook și Youtube

Meniu