Ecuația de forma ax+b =0, a,b ϵ R, a≠0

x este necunoscuta, iar a și b se numesc coeficienți. b se mai numește termenul liber.

Soluția ecuației este x= 

Două ecuații se numesc echivalente dacă au aceeași soluție.

Exemplu:

Rezolvați, în R, următoarea ecuație: 2x+5=4x-3

Mutăm totți termenii în partea stângă:

2x+5-4x+3=0

-2x+8=0

Identificăm coeficienții:

a=-2, b=8.

Calculăm necunoscuta:

x =  = 

x = 4

Scriem soluția ecuației:

S={4}

Sisteme de două ecuații liniare cu două necunoscute

Sistemele de două ecuații liniare cu două necunoscute au forma:

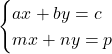
a,b,c,m,n,p ϵ R.

Două sisteme de ecuații se numesc echivalente dacă au aceeași mulțime a soluțiilor.

Exemplu:

Rezolvați, în R, următorul sistem de ecuații:

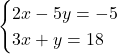
Metoda substituției

Se prelucrează una dintre ecuații, pentru a scoate una dintre necunoscute, în funcție de cealaltă:

2x=-5+5y

x = 

Se înlocuiește necunoscuta scoasă mai sus, în cealaltă ecuație, se aduce la o formă cât mai simplă, și astfel se detremină cealaltă necunoscută:

3x + y = 18

3·

-15+17y=18·2

-15+17y=36

17y=36 + 15

17y=51

y=51:17

y=3

Se determină și necunoscuta substituită inițial:

x= 5

Se scrie soluția sistemului: S={(5;3)}

Metoda reducerii

Se înmulțesc ambele ecuații cu câte un număr nenul, astfel încât, dacă adunăm cele două ecuații, termenii care conțin una dintre necunoscute să se reducă.

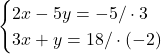
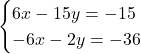
Se adună cele două ecuații astfel obținute, astfel se determină una dintre necunoscute:

Se înlocuiește necunoscuta aflată, într-una dintre ecuații, pentru a afla cealaltă necunoscută:

Se scrie soluția sistemului: S={(5;3)}