Proprietățile dreptunghiului:

Fiind un paralelogram, dreptunghiul are toate proprietățile paralelogramului (vezi aici care sunt proprietățile paralelogramului), dar are și proprietăți particulare:

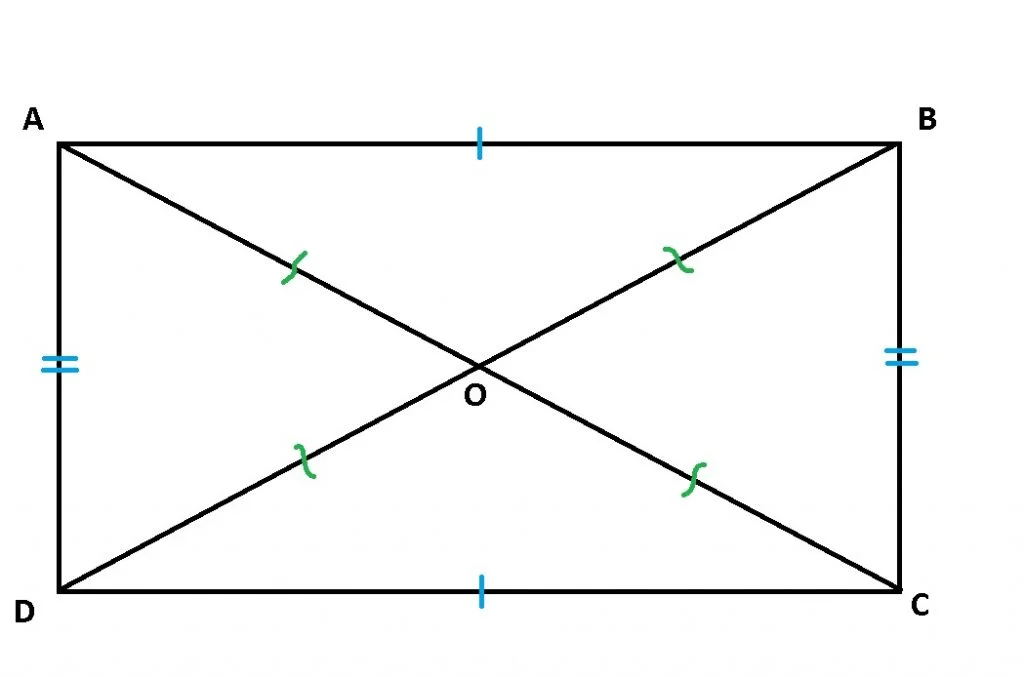
ABCD – dreptunghi:

• Toate unghiurile au 90°: m∢A=m∢B=m∢C=m∢D=90°;
• Diagonalele sunt congruente: AC=BD;
• laturile opuse sunt paralele și congruente două câte două;
  AB=CD și BC=AD; AB||CD și BC||AD;
• diagonalele se înjumătățesc: AO=BO=CO=DO, unde {O}=AC∩BD.
•  

Cum demonstrez că un patrulater convex este dreptunghi:

• Mai întâi demonstrăm că patrulaterul este paralelogram (vezi aici cum arătăm că un patrularter convex este paralelogram)
• Arătăm că paralelogramul este dreptunghi, folosind una dintre proprietățile de mai jos:
  
  • are un unghi de 90°;
  • are diagonalele congruente.
  •  

Rombul

Rombul este paralelogramul cu două laturi consecutive congruente.

Proprietățile rombului:

Fiind un paralelogram, rombul are toate proprietățile paralelogramului (vezi aici care sunt proprietățile paralelogramului), dar are și proprietăți particulare:

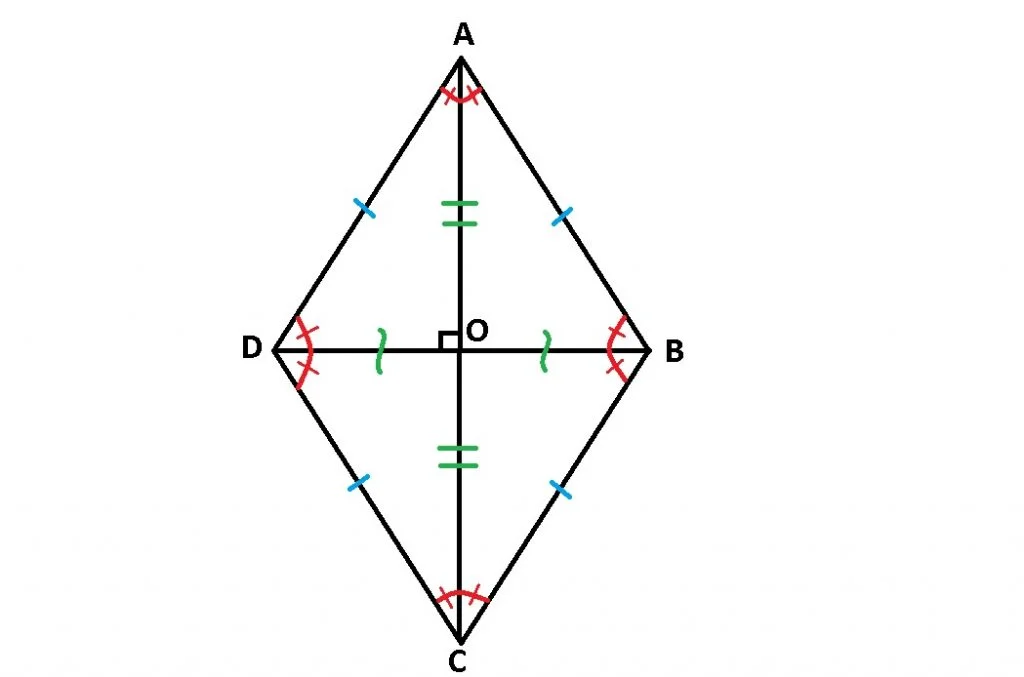
ABCD – romb:

• Toate laturile sunt congruente: AB=BC=CD=DA;
• Diagonalele sunt perpendiculare: AC⊥BD;
• Diagonalele sunt bisectarele unghiurilor: AC=bis.∢A și bis.∢C, BD=bis.∢B și bis.∢D;
• laturile opuse sunt paralele două câte două AB||CD și BC||AD;
• diagonalele se înjumătățesc: AO=BO=CO=DO, unde {O}=AC∩BD;
• unghiurile opuse sunt congruente: m∢A=m∢C, m∢B=m∢D;
• unghiurile alăturate sunt suplementare.
•  

Cum demonstrez că un patrulater convex este romb:

• Mai întâi demonstrăm că patrulaterul este paralelogram (vezi aici cum arătăm că un patrularter convex este paralelogram)
• Arătăm că paralelogramul este romb, folosind una dintre proprietățile de mai jos:
  
  • are două laturi consecutive congruente;
  • are diagonalele perpendiculare;
  • una dintre diagonale este bisectoare.
  •  

Pătratul

Pătratul este paralelogramul cu toate laturile și toate unghiurile congruente. Pătratul este și dreptunghi și romb.

Proprietățile pătratului:

Fiind un paralelogram, pătratul are toate proprietățile paralelogramului (vezi aici care sunt proprietățile paralelogramului), dar are și proprietăți particulare:

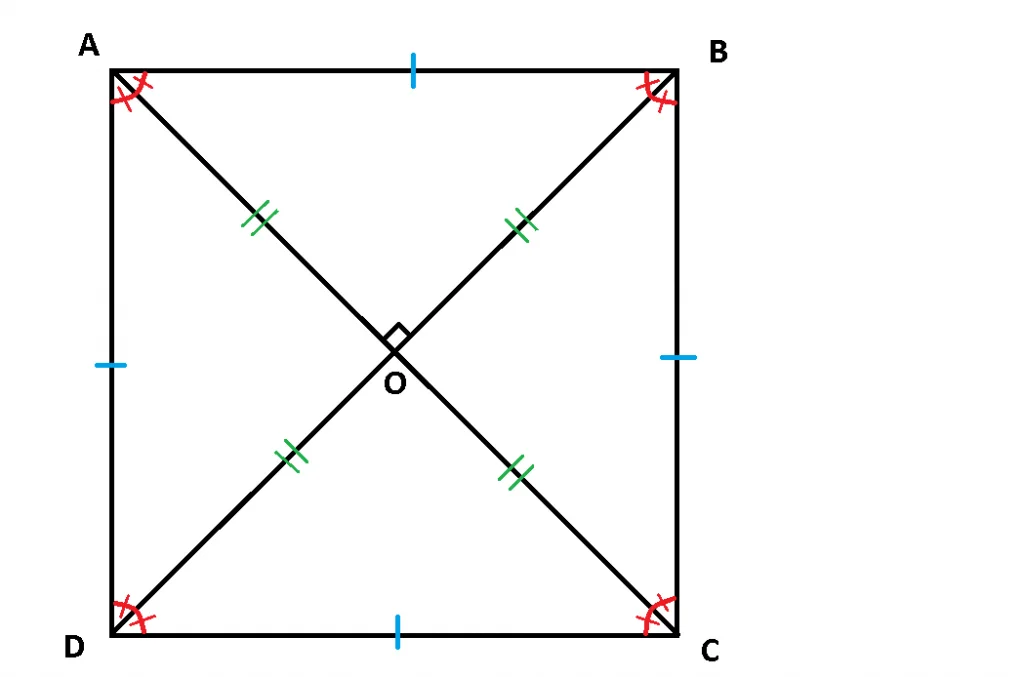
ABCD – pătrat:

• Toate unghiurile au 90°: m∢A=m∢B=m∢C=m∢D=90°;
• Toate laturile sunt congruente: AB=BC=CD=DA;
• Diagonalele sunt congruente: AC=BD;
• Diagonalele sunt perpendiculare: AC⊥BD;
• Diagonalele sunt bisectare: AC=bis∢A și bis∢C, BD=bis∢B și bis∢D;
• laturile opuse sunt paralele două câte două AB||CD și BC||AD;
• diagonalele se înjumătățesc: AO=BO=CO=DO, unde {O}=AC∩BD.
•  

Cum demonstrez că un patrulater convex este pătrat:

• Mai întâi demonstrăm că patrulaterul este paralelogram (vezi aici cum arătăm că un patrularter convex este paralelogram)
• Arătăm că paralelogramul este romb, folosind una dintre proprietățile de mai jos:
  
  • are două laturi consecutive congruente;
  • are diagonalele perpendiculare;
  • una dintre diagonale este bisectoare.
• Și apoi arătăm că rombul este și dreptunghi, folosind una dintre proprietățile de mai jos:
  
  • are un unghi de 90°;
  • are diagonalele congruente.
  •  

Utilizare paralelograme particulare

Paralelogramele particulare sunt forme geometrice care au proprietăți specifice și sunt utilizate în diverse domenii pentru rezolvarea unor probleme specifice. Aceste forme particulare de paralelograme sunt dreptunghiurile, pătratele, romburile.

Dreptunghiurile sunt paralelograme cu unghiurile drept, ceea ce le face foarte utile în construcții, deoarece acestea pot fi ușor montate și utilizate ca bază pentru clădiri, poduri și alte structuri.

Pătratele sunt dreptunghiuri cu laturile egale, ceea ce le face să fie foarte utile în construcții, deoarece acestea pot fi ușor montate și utilizate ca bază pentru clădiri, poduri și alte structuri, precum și în grafică și design.

Romburile sunt paralelograme și sunt utile în construcții, unde sunt utilizate pentru a forma modele decorative sau pentru a îmbunătăți rezistența structurilor.

În concluzie, paralelogramele particulare, incluzând dreptunghiurile, pătratele, romburile, sunt forme geometrice importante cu proprietăți specifice și aplicații în diverse domenii, precum construcții, grafică și design.