Trapezul
Trapezul este patrulaterul convex care are două laturi opuse paralele și celelalte două laturi opuse neparalele.
Acest material despre trapez cuprinde următoarele noțiuni: definiția trapezului, linia mijlocie în trapez, trapezul oarecare, trapezul isoscel și trapezul dreptunghic.

Trapezul, Definiție
Trapezul este patrulaterul convex care are două laturi opuse paralele și celelalte două laturi opuse neparalele.
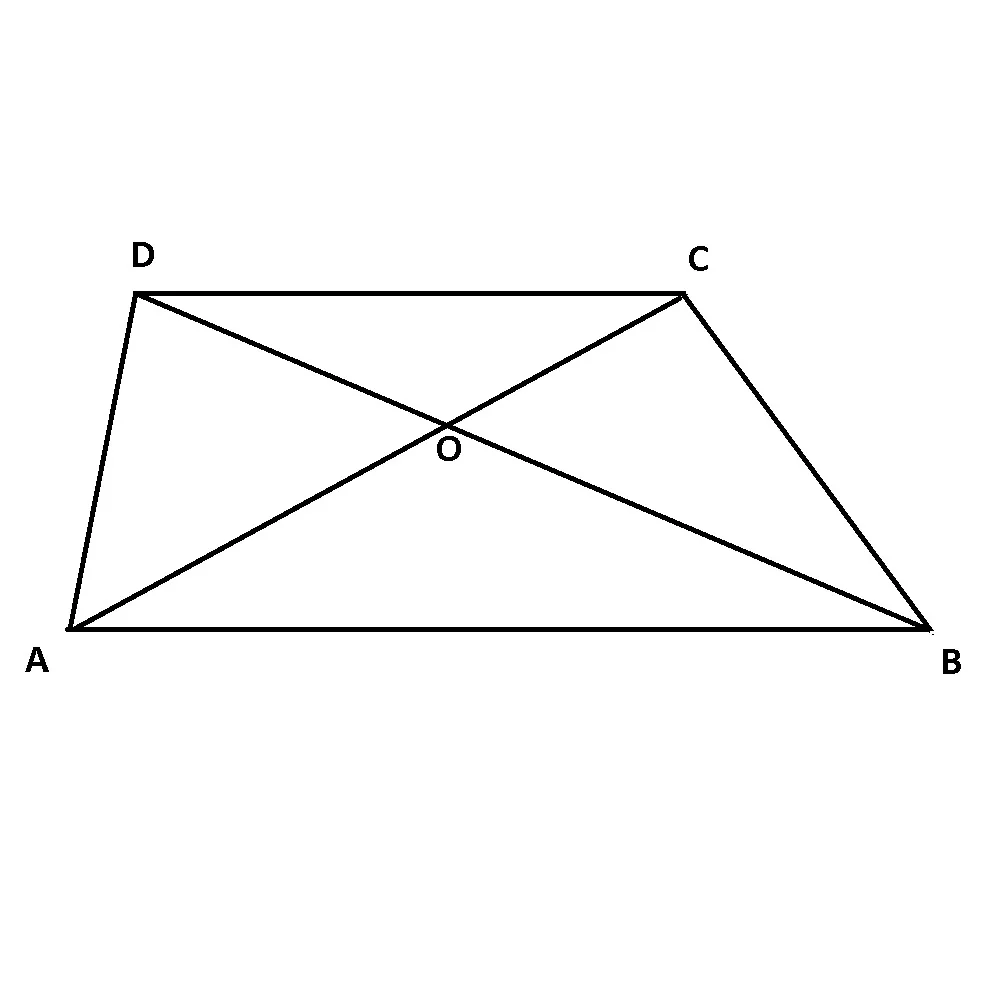
Dacă ABCD este un patrulater convex cu AB || CD și BC∦AD, atunci ABCD este un trapez.
Laturile paralele se numesc baze: AB este baza mare (B), iar CD este baza mică (b); AC și BD sunt diagonalele trapezului.
Unghiurile alăturate unei laturi neparalele sunt suplementare: m∢A+m∢D= m∢B+m∢C= 180°.
Linia mijlocie în trapez
Linia mijlocie în trapez este segmentul care unește mijloacele laturilor neparalele ale trapezului.
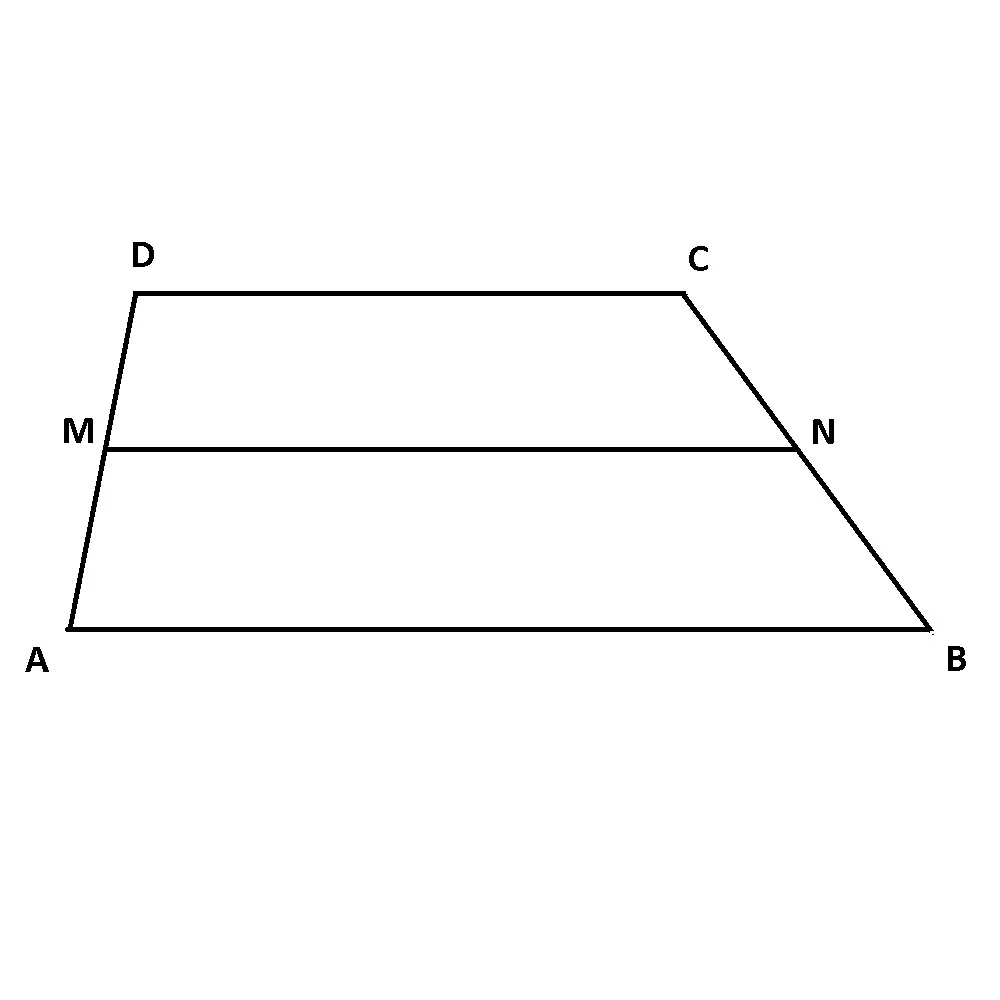
ABCD trapez cu AB || CD:
Dacă M este mijlocul lui AD și N este mijlocul lui BC, atunci MN este linie mijlocie în trapezul ABCD.
Linia mijlocie este paralelă cu bazele trapezului și lungimea sa este egală semisuma lungimilor bazelor.
Dacă MN este linie mijlocie în trapezul ABCD, atunci: MN || AB, MN || CD și MN=![]()
Înălțimea în trapez
Înalțimea trapezului este un segment determinat de punctele de intersecție ale bazelor cu o perpendiculară dusă pe ele.
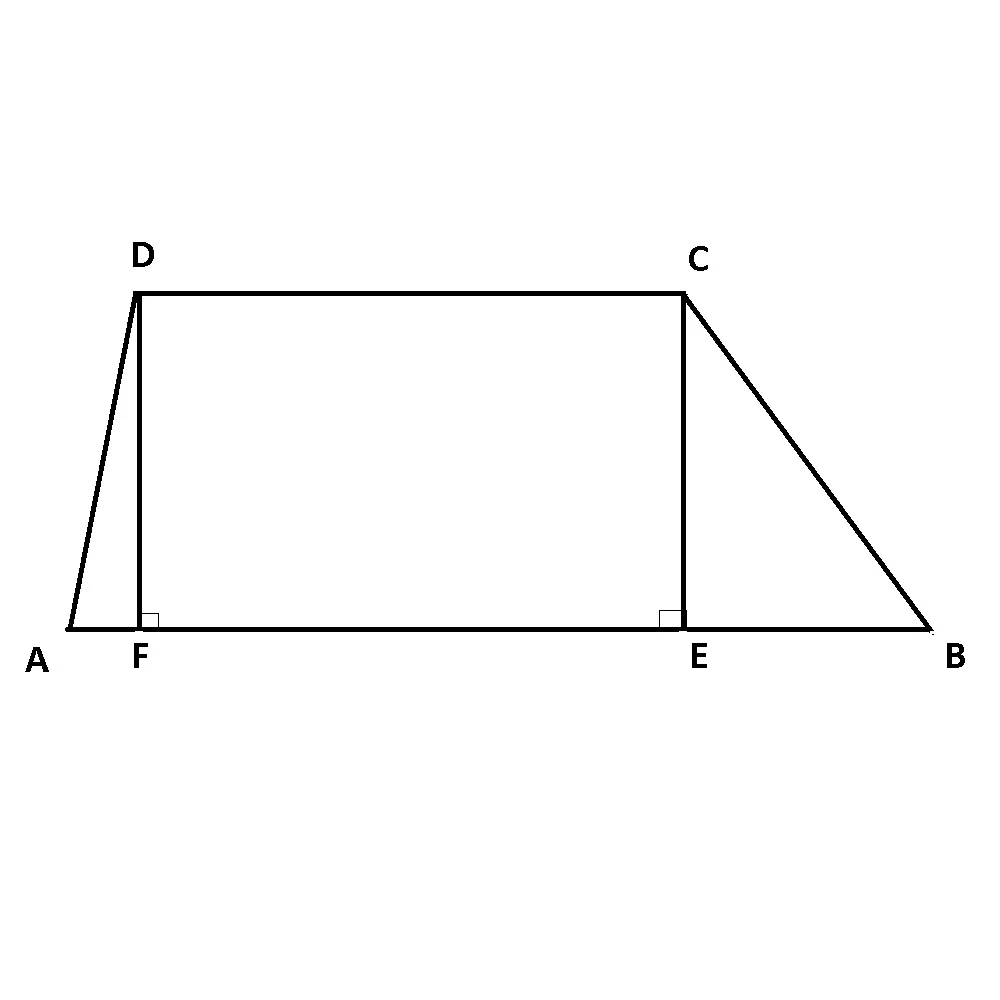
În trapezul ABCD cu AB || CD:
CE⊥ AB, E∈AB ⇒ CE = h (înălțime în trapezul ABCD)
DF⊥ AB, F∈AB ⇒ DF = h (înălțime în trapezul ABCD).
Trapezul, Clasificare
Trapezul oarecare
Trapezul oarecare este trapezul care are laturile neparalele de lungimi diferite și care nu are unghiuri drepte:
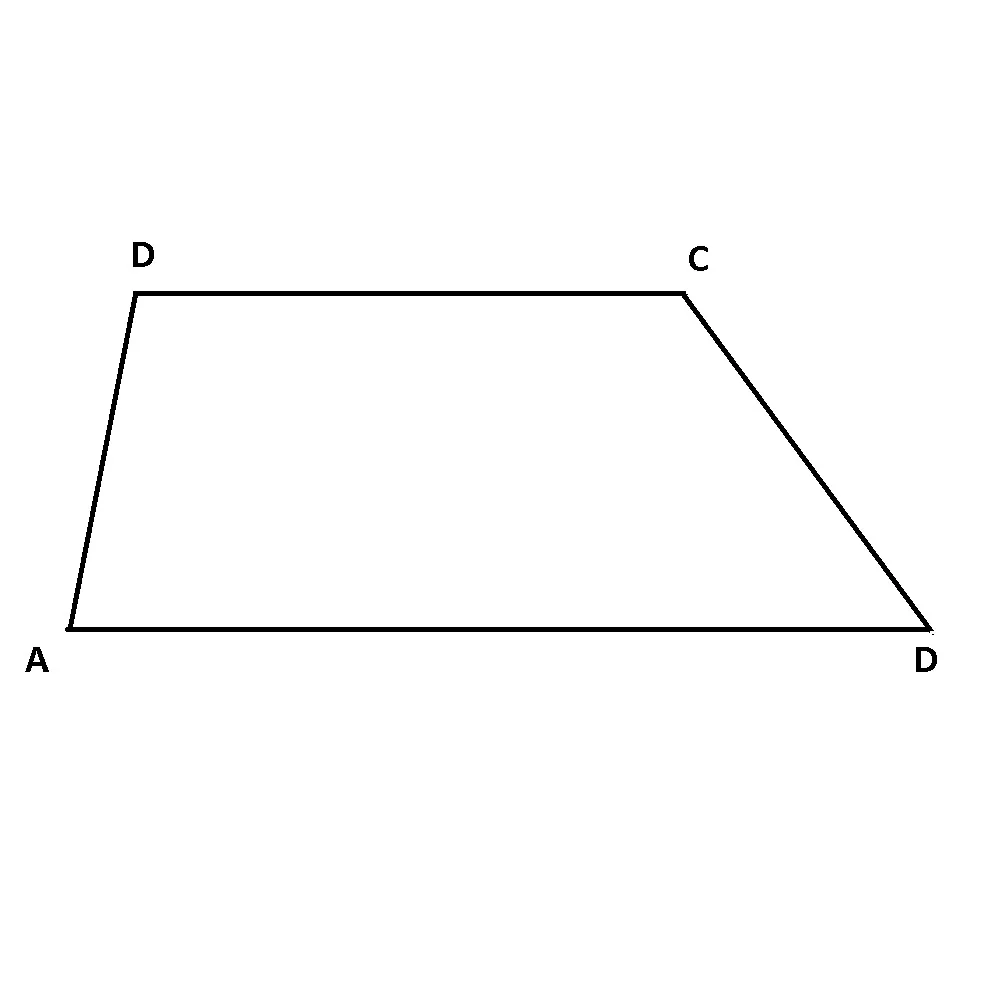
ABCD trapez oarecare (cu AB || CD): BC ≠AD, m∢A≠90°, m∢B≠90°, m∢C≠90°, m∢D≠90°.
Trapezul isoscel
Trapezul isoscel este trapezul cu laturile neparalele congruente.
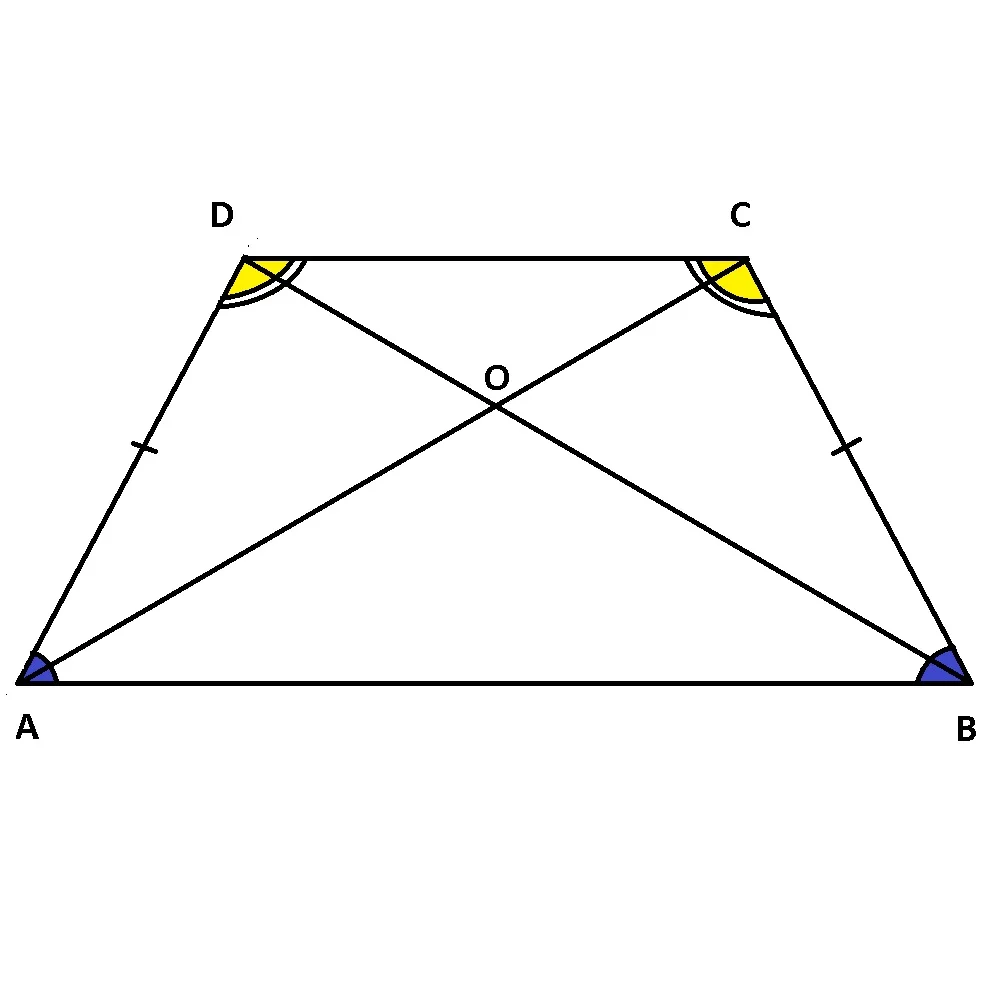
Dacă ABCD este un trapez cu AB || CD și BC=AD, atunci ABCD este un trapez isoscel.
Proprietăți:
- unghiurile alăturate unei baze sunt congruente: m∢A=m∢B și m∢C=m∢D
- diagonalele sunt congruente: AC=BD
Trapezul dreptunghic
Trapezul dreptunghic este trapezul care are o latură neparalelă perpendiculară pe baze.
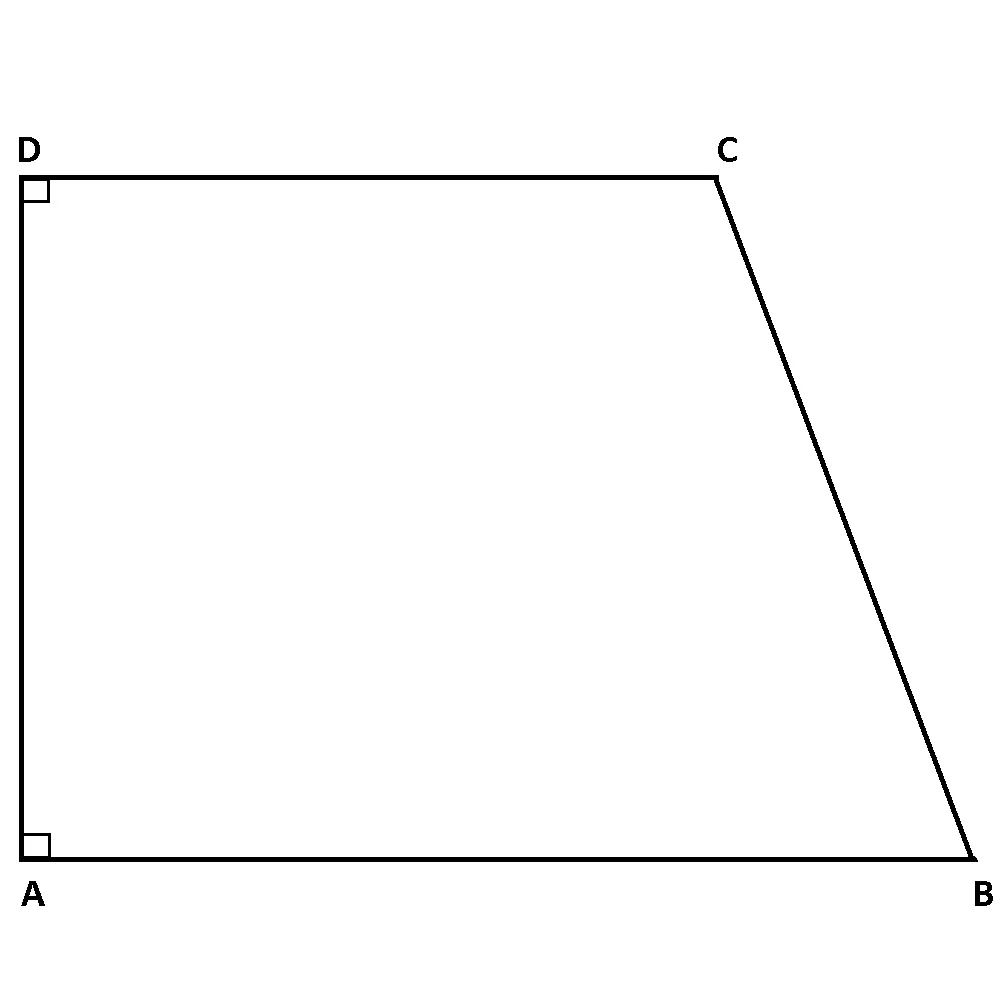
Dacă ABCD este un trapez cu AB || CD, în care AD⊥ AB și AD⊥ CB, atunci ABCD este un trapez dreptunghic.
m∢A = m∢D= 90°.
Trapezul, Utilizare
Trapezul este o formă geometrică specială, alcătuită din două laturi paralele și două laturi oblice. Acest lucru îl face să fie foarte versatil și utilizat în diverse domenii pentru rezolvarea unor probleme specifice.
În matematică, trapezul este utilizat în calculul ariei și al perimetrului, precum și în rezolvarea unor probleme legate de proporții, raporturi și funcții. De asemenea, este folosit în geometrie pentru a studia formele și proprietățile geometrice ale formelor.
În construcții, trapezul este utilizat pentru a crea acoperișuri inclinate sau pentru a forma baze pentru structuri. De asemenea, este folosit în designul de interior și exterior pentru a crea forme decorative sau pentru a adăuga stabilitate structurii.
În grafică și design, trapezul este folosit pentru a crea forme interesante și pentru a îmbunătăți aspectul general al unui proiect. De asemenea, poate fi folosit pentru a crea forme de bază care pot fi apoi modificate pentru a crea modele unice și interesante.
În concluzie, trapezul este o formă geometrică importantă cu proprietăți specifice și aplicații în diverse domenii, precum matematică, construcții, grafică și design. Utilizarea acestei forme poate ajuta la rezolvarea unor probleme specifice și la crearea de forme unice și atractive.

