Arii și volume ale piramidelor
În cele ce urmează, vă prezentăm formulele pentru arii și volume ale piramidelor: piramida triunghiulară regulată, piramida patrulateră regulată, piramida hexagonală regulată și tetraedrul regulat.

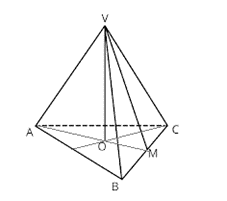
O piramidă este un obiect geometric tridimensional care are o bază poligonală plană și fețe laterale care se intersectează într-un punct vârf, formând o structură în formă de triunghi sau poligon. Elementele componente ale unei piramide includ:
Baza: Este poligonul plan care servește ca fundație a piramidei și care determină forma de bază a acesteia. Baza poate fi orice poligon convex, cum ar fi un triunghi, un pătrat, un pentagon sau un poligon cu mai multe laturi.
Vârful: Este punctul în care fețele laterale ale piramidei se întâlnesc și este opusul bazei. Vârful este singurul punct care nu aparține planului bazei.
Fețe laterale: Acestea sunt suprafețele laterale ale piramidei care se extind de la laturile bazei la vârful piramidei. Fețele laterale sunt triunghiuri sau poligoane care se întâlnesc în vârf.
Înălțimea: Este distanța verticală de la vârf la planul bazei, măsurată perpendicular pe baza piramidei. Lungimea acestei înălțimi poate varia în funcție de tipul piramidei și de forma bazei.
Piramidele pot fi clasificate în funcție de forma bazei și de simetria fețelor laterale. Ele pot fi regulate sau neregulate, în funcție de simetria și mărimile laturilor bazei, și pot fi triunghiulare, patrulatere, pentagonale, hexagonale sau cu un număr mai mare de laturi.
Piramida triunghiulară regulată
Aria bazei: Ab = ![]()
Perimetrul bazei: Pb = 3l
Aria laterală: Al = ![]() (ap=apotema piramidei)
(ap=apotema piramidei)
Aria totală: At = Ab + Al;
Volumul: V = ![]() (h=înălțimea piramidei)
(h=înălțimea piramidei)
Piramida patrulateră regulată
Aria bazei: Ab = ![]()
Perimetrul bazei: Pb = 4l
Aria laterală: Al = ![]() (ap=apotema piramidei)
(ap=apotema piramidei)
Aria totală: At = Ab + Al;
Volumul: V = ![]() (h=înălțimea piramidei)
(h=înălțimea piramidei)
Piramida hexagonală regulată
Aria bazei: Ab = ![]()
Perimetrul bazei: Pb = 6l
Aria laterală: Al = ![]() (ap=apotema piramidei)
(ap=apotema piramidei)
Aria totală: At = Ab + Al;
Volumul: V = ![]() (h=înălțimea piramidei)
(h=înălțimea piramidei)
Tetraedrul regulat
Aria bazei: Ab = ![]()
Perimetrul bazei: Pb = 3l
Aria laterală: Al = ![]() sau Al =
sau Al = ![]()
Aria totală: At = Ab + Al sau At = ![]()
Volumul: V = ![]() sau V =
sau V = ![]()
Utilizare Arii și volume ale piramidelor
Piramidele sunt forme geometrice fascinante, cu proprietăți matematice și aplicații practice remarcabile în diverse domenii. Atât aria cât și volumul piramidelor sunt concepte esențiale în geometrie și au o gamă largă de utilizări în viața reală. În acest articol, vom explora câteva dintre modurile în care aria și volumul piramidelor sunt utilizate în practică.
1. Arhitectură și Construcții
Piramidele sunt un simbol iconic al arhitecturii antice și sunt adesea folosite ca inspirație pentru structurile moderne. În arhitectură și construcții, cunoștințele despre aria și volumul piramidelor sunt esențiale în proiectarea și construcția clădirilor, monumentelor și structurilor ornamentale.
Cunoașterea ariei bazei și înălțimii piramidei este crucială pentru calcularea materialelor necesare și determinarea costurilor de construcție. De asemenea, cunoașterea volumului piramidei este importantă în planificarea spațiilor interioare și exterioare, precum și în determinarea capacității și utilizării acestora.
2. Geodezie și Topografie
În domeniul geodeziei și topografiei, aria și volumul piramidelor sunt utilizate pentru a calcula și măsura terenurile și structurile înclinate. Piramidele trunchiate, de exemplu, sunt adesea folosite ca repere topografice pentru măsurarea și cartografierea reliefului terenului.
Cunoașterea ariei și volumului piramidelor ajută topografii să înțeleagă și să reprezinte corect dimensiunile și formele terenului în hărți și planuri, fiind esențială pentru planificarea urbană, amenajarea teritoriului și gestionarea resurselor naturale.
3. Industria Alimentară și Agricolă
În industria alimentară și agricolă, aria și volumul piramidelor sunt utilizate pentru a calcula și estima cantitățile de produse alimentare și agricole. De exemplu, în depozite și silozuri, cunoașterea volumului piramidelor este esențială pentru stocarea și gestionarea eficientă a cerealelor, semințelor și altor produse agricole.
De asemenea, cunoștințele despre aria piramidelor sunt utile în domeniul procesării alimentelor, contribuind la calcularea și optimizarea rețetelor și a proporțiilor de ingrediente pentru producția alimentară la scară industrială.
Concluzie
Aria și volumul piramidelor sunt concepte matematice fundamentale cu o gamă largă de utilizări în viața reală, de la arhitectură și construcții până la geodezie și industria alimentară. Cunoștințele despre aceste concepte sunt esențiale pentru proiectarea, construcția, cartografierea și gestionarea eficientă a resurselor în diverse domenii. Prin urmare, este important să recunoaștem importanța și relevanța acestor concepte și să le integrăm în mod corespunzător în practica noastră cotidiană pentru a facilita progresul și inovația în diverse domenii.

