Arii și volume ale prismelor 📚

Arii și volume ale prismelor

Acest material despre arii și volume ale prismelor include următoarele noțiuni: prisma triunghiulară regulată, prisma patrulateră regulată, prisma hexagonală regulată, paralelipipedul dreptunghic, cubul.

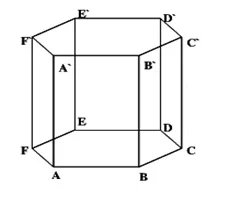
O prismă este un corp geometric tridimensional format din două planuri paralele și poligoane identice situate în aceleași plane, numite baze, și fețe laterale care sunt paralelograme. Prin urmare, o prismă este caracterizată de următoarele elemente:

Baze: Sunt două poligoane identice care sunt situate în planuri paralele. Acestea pot fi orice poligoane regulate sau neregulate și formează fețele opuse ale prismei.
Fețe laterale: Acestea sunt suprafețele laterale ale prismei care conectează fiecare latură a bazei superioare cu latura corespunzătoare a bazei inferioare. Fețele laterale sunt paralelograme și sunt întotdeauna plane.
Înălțimea: Este distanța verticală între planele bazelor și reprezintă lungimea segmentului perpendicular între planele bazei. Înălțimea poate varia în funcție de forma și dimensiunile prismei.

Pentru a clasifica o prismă, putem lua în considerare forma și tipul bazelor și numărul de laturi ale acestora. Prin urmare, o prismă poate fi rectangulară, pătrată, triunghiulară, hexagonală sau cu un număr mai mare de laturi, în funcție de forma bazelor sale. De asemenea, prismele pot fi regulate sau neregulate, în funcție de simetria fețelor și a bazelor.

Prisma triunghiulară regulată

Aria bazei: A_b = $\dfrac{l^2\sqrt{3}}{4}$

Perimetrul bazei: P_b= 3l

Aria laterală: Al = $Pb \cdot h$ (h=înălțimea prismei)

Aria totală: At = 2Ab + Al;

Volumul: V = $Ab\cdot h$ (h=înălțimea prismei)

Prisma patrulateră regulată

Aria bazei: A_b = $l^2$

Perimetrul bazei: P_b= 4l

Aria laterală: Al = $Pb \cdot h$ (h=înălțimea prismei)

Aria totală: At = 2Ab + Al;

Volumul: V = $Ab\cdot h$ (h=înălțimea prismei)

Prisma hexagonală regulată

Aria bazei: A_b = $\dfrac{3l^2\sqrt{3}}{2}$

Perimetrul bazei: P_b= 6l

Aria laterală: Al = $Pb \cdot h$ (h=înălțimea prismei)

Aria totală: At = 2Ab + Al;

Volumul: V = $Ab\cdot h$ (h=înălțimea prismei)

Paralelipipedul dreptunghic

Aria bazei: A_b = $L \cdot l$

Perimetrul bazei: P_b= 2(L+l)

Aria laterală: Al = $Pb \cdot h$

Aria totală: At = 2Ab + Al;

Volumul: V = $Ab\cdot h$ sau V = $L \cdot l \cdot h$

Cubul

Aria bazei: A_b = $l^2$

Perimetrul bazei: P_b= 4l

Aria laterală: Al = $4l^2$

Aria totală: At = $6l^2$

Volumul: V = $l^3$

Utilizare Arii și volume ale prismelor

Prismele sunt forme geometrice tridimensionale cu o varietate de aplicații practice în viața reală. Aria și volumul prismelor sunt concepte matematice esențiale care sunt utilizate în diverse domenii, de la arhitectură și inginerie la design industrial și construcții. În acest articol, vom explora câteva dintre modurile în care aria și volumul prismelor sunt utilizate în practică.

1. Ambalaje și Logistică

Prismele sunt folosite adesea în industria ambalajelor și logistică pentru a stoca și transporta produse într-un mod eficient. Cutiile și containerele, care au forma unei prisme, sunt proiectate pentru a maximiza spațiul disponibil și pentru a reduce pierderile de spațiu în timpul transportului și depozitării.

Cunoștințele despre aria și volumul prismelor sunt esențiale pentru a determina dimensiunile optime ale ambalajelor și containerele, precum și pentru a calcula capacitatea de stocare și încărcare a acestora. Aceste informații contribuie la optimizarea proceselor de ambalare și logistică, reducând costurile și riscurile asociate cu manipularea și transportul mărfurilor.

2. Arhitectură și Construcții

În domeniul arhitecturii și construcțiilor, aria și volumul prismelor sunt utilizate pentru a calcula și planifica spațiile interioare și exterioare ale clădirilor și structurilor. Prismele sunt adesea folosite ca elemente de bază în proiectarea și construcția clădirilor, datorită simplității lor și a versatilității.

Cunoașterea ariei și volumului prismelor este crucială pentru a determina cantitatea de materiale necesare pentru construcția lor, precum și pentru a evalua costurile și eficiența proiectelor. De asemenea, aceste informații sunt utile pentru a planifica distribuția spațiilor și a optimiza funcționalitatea și confortul clădirilor.

3. Industria Alimentară și Farmaceutică

În industria alimentară și farmaceutică, aria și volumul prismelor sunt utilizate pentru a calcula și estima cantitățile de produse și substanțe necesare pentru producție și îmbuteliere. De exemplu, rezervoarele și recipientele care au forma unei prismele sunt folosite pentru stocarea și distribuirea lichidelelor și pulberilor în cadrul proceselor industriale.

Cunoașterea ariei și volumului prismelor este esențială pentru a determina capacitatea și eficiența acestor recipiente, precum și pentru a calcula dozele și proporțiile de substanțe necesare pentru producție. Aceste informații contribuie la asigurarea calității și consistenței produselor finite și la optimizarea proceselor de fabricație.

Concluzie

Aria și volumul prismelor sunt concepte matematice fundamentale cu o varietate de aplicații practice în viața reală. Utilizarea acestor concepte în diverse domenii, cum ar fi ambalajele și logistică, arhitectura și construcțiile, sau industria alimentară și farmaceutică, contribuie la optimizarea proceselor și la îmbunătățirea eficienței și calității produselor și serviciilor. Prin urmare, este important să recunoaștem importanța și relevanța acestor concepte și să le integrăm în mod corespunzător în practica noastră cotidiană pentru a facilita progresul și inovația în diverse domenii.

Dacă îți place platforma noastră, te invit și pe pagina noastră de Facebook și Youtube

Meniu