Noțiuni de bază privind puncte, drepte și plane

•  Prin două puncte distincte trece o dreaptă și numai una.

           A ≠ B; A,B ϵ d  => AB=BA=d    

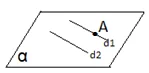
• Într-un plan, printr-un punct exterior unei drepte, se poate duce o paralelă și numai una la dreapta dată. Oricare două drepte paralele sunt coplanare. (adică se află în același plan)

          Dacă A∉d2, există o unică dreaptă d1, pentru care A ϵ d1 și d1||d2

          d1 ⸦ α și d2 ⸦ α.

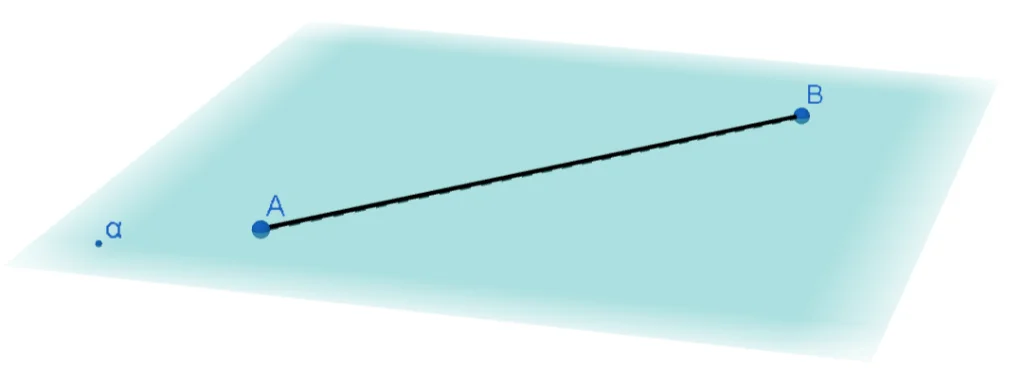
• Dacă două puncte distincte aparțin unui plan, atunci și dreapta determinată de acele puncte este inclusă în acel plan.

Dacă A ϵ α și B ϵ α, A≠B, atunci AB ⸦ α.

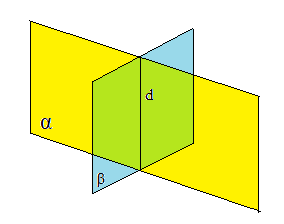
• Dacă două plane se intersectează, intersecția lor este o dreaptă.

α ∩ ꞵ = {d}.

Determinarea planului

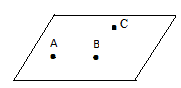
• Trei puncte necoliniare determină un plan: Dacă A,B,C necoliniare, putem determina planul (ABC).

• O dreaptă și un punct exterior ei determină un plan: Dacă A∉d, atunci putem determina planul (A,d)

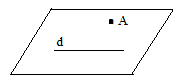
• Două drepte concurente determină un plan: Dacă d1∩d2={O}, atunci putem determina planul (d1,d2)

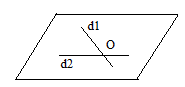
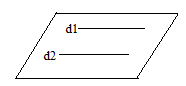
• Două drepte paralele determină un plan: Dacă d1||d2, atunci putem determina planul (d1,d2)

Pozițiile relative a două drepte în spațiu

• Drepte concurente = sunt coplanare și se intersectează într-un punct: d1∩d2={O}, d1,d2⸦ α

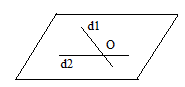
• Drepte paralele = sunt coplanare și nu au niciun punct comun: d1 | | d2; d1,d2⸦ α

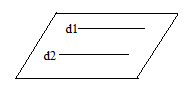
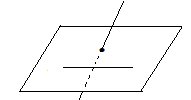
• Drepte necoplanare = nu sunt incluse în același plan, nu sunt paralele, dar nici concurente

Utilizare Geometrie în spațiu

Geometria, o ramură fundamentală a matematicii, ne ajută să înțelegem și să lucrăm cu formele și structurile din jurul nostru. În timp ce mulți dintre noi ne gândim la geometrie în contextul planului bidimensional, aceasta joacă un rol crucial și în explorarea spațiului tridimensional. În realitate, aplicațiile geometriei în spațiu sunt vaste și diverse, influențând domenii precum arhitectura, navigația, ingineria și multe altele. Așadar, să aruncăm o privire mai atentă asupra modului în care geometria în spațiu își găsește locul în viața noastră cotidiană.

• Unul dintre cele mai evidente exemple de utilizare a geometriei în spațiu este în domeniul arhitecturii și designului. Arhitecții folosesc principiile geometrice pentru a crea structuri impresionante și funcționale. De la calcularea unghiurilor și proporțiilor în proiectarea unei clădiri până la analizarea spațiului tridimensional pentru a maximiza lumina naturală și eficiența energetică, geometria este la baza fiecărui aspect al procesului de design arhitectural.
• În domeniul ingineriei și construcțiilor, geometria în spațiu este esențială pentru a construi structuri solide și sigure. Inginerii folosesc concepte geometrice pentru a calcula forțele și tensiunile care acționează asupra materialelor de construcție și pentru a proiecta structuri care să reziste la aceste presiuni. De la punți și autostrăzi până la clădiri și stații spațiale, geometria în spațiu este prezentă în fiecare fază a procesului de construcție.
• Geometria în spațiu este la baza sistemelor de navigație și cartografie moderne. GPS-ul, sau Sistemul de Poziționare Globală, utilizează principiile geometrice pentru a determina poziția exactă a unui obiect în spațiu. Calculând distanțele și unghiurile dintre receptorul GPS și mai multe sateliți, sistemul poate determina poziția cu o precizie extraordinară, facilitând navigarea în spațiu și pe suprafața Pământului.
• În domeniul medicinii, geometria în spațiu este folosită în imagistica medicală pentru a obține imagini precise ale structurilor interne ale corpului uman. Tomografia computerizată și rezonanța magnetică utilizează algoritmi geometrici pentru a reconstrui imagini tridimensionale ale organelor și țesuturilor, ajutând medicii să diagnosticheze și să trateze diferite afecțiuni.

Concluzie

Geometria în spațiu este mult mai mult decât o abstracție matematică; este o unealtă practică și esențială în viața noastră de zi cu zi. De la proiectarea structurilor arhitecturale și navigarea în spațiu până la diagnosticarea bolilor și dezvoltarea tehnologiilor avansate, geometria în spațiu ne ajută să înțelegem și să explorăm lumea din jurul nostru într-un mod precis și eficient. Prin aplicarea conceptelor geometrice în diferite domenii, continuăm să descoperim și să valorificăm potențialul acestora pentru a îmbunătăți calitatea vieții noastre și pentru a avansa în cunoașterea umană.