Geometrie în spațiu: pozițiile relative a două drepte, unghiul a două drepte, pozițiile unei drepte față de un plan
Geometrie în spațiu: pozițiile relative a două drepte în spațiu, relația de paralelism în spațiu, unghiuri cu laturile respectiv paralele, unghiul a două drepte în spațiu, drepte perpendiculare, pozițiile relative ale unei drepte față de un plan.

Pozițiile relative a două drepte în spațiu
Două drepte care au un singur punct comun se numesc drepte concurente.
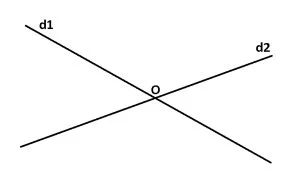
d1 ∩ d2 = {O}
Două drepte care se află în același plan și care nu au niciun punct comun se numesc drepte paralele.
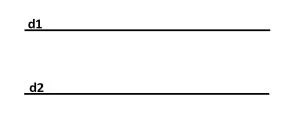
d1 || d2
Două drepte situate în același plan se numesc drepte coplanare.
Două drepte care nu sunt nici concurente și nici paralele sunt drepte necoplanare.
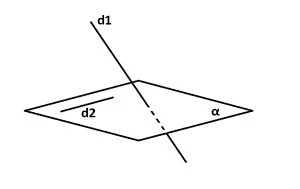
d1 ∩ d2 = Ø
d1 ∦ d2
Tranzitivitatea relației de paralelism în spațiu
Dacă două drepte distincte sunt paralele cu o a treia dreaptă , atunci dreptele sunt paralele între ele.

d1 || d3 și d2 || d3 => d1 || d2
Unghiul a două drepte în spațiu
Două unghiuri cu laturile respectiv paralele sunt:
- congruente (dacă amandouă sunt ascuțite sau amandouă sunt obtuze)
- suplementare (dacă unul dintre unghiuri este obtuz și celălalt ascuțit)
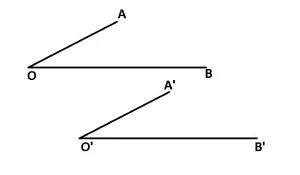
AO || A’O’
BO || B’O’
m![]() AOB = m
AOB = m![]() A’O’B’
A’O’B’
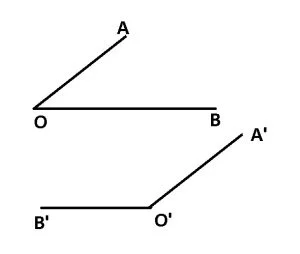
AO || A’O’
BO || B’O’
m![]() AOB + m
AOB + m![]() A’O’B’ = 180°
A’O’B’ = 180°
Unghiul a două drepte în spațiu reprezintă unghiul ascuțit sau drept cu vârful în orice punct al planului și cu laturile respectiv paralele cu dreptele date.
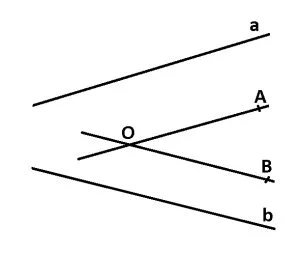
AO || a, BO || b și AO ∩ BO = {O} => m (a;b) = m
(a;b) = m (AO;OB) = m
(AO;OB) = m AOB
AOB
Observație: unghiul dintre două drepte paralele are măsura de 0°.
Dacă măsura unghiului a două drepte în spațiu este de 90°, atunci ele se numesc drepte perpendiculare.
Pozițiile relative ale unei drepte față de un plan
- Dacă o dreaptă are două puncte comune cu un plan, atunci dreapta este conținută în acel plan.
- Dacă o dreaptă are un punct comun cu un plan, atunci dreapta intersectează planul.
- Dacă o dreaptă nu are niciun punct comun cu un plan, atunci dreapta este paralelă cu planul
- Teoremă: Dacă o dreaptă este paralelă cu o dreaptă din plan, atunci dreapta este paralelă cu planul.
Dreaptă conținută în plan:
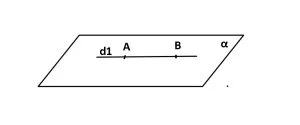
A și B ∈ α
A și B ∈ d
=> d ⊂ α
Dreaptă intersectată cu planul
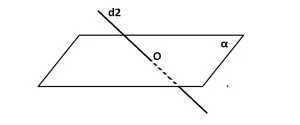
d2 ∩ α = {O}
Dreaptă paralelă cu planul
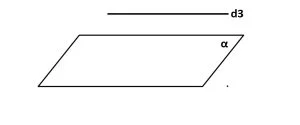
d3 ∩ α = Ø => d3 || α
O dreaptă este paralelă cu un plan dacă este paralelă cu o dreaptă conținută de acel plan.
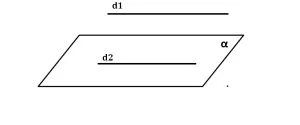
d1 || d2 și d2 ⊂ α => d1 || α
Utilizare Geometrie în spațiu
Geometria în spațiu, o ramură fascinantă a matematicii, studiază formele și proprietățile obiectelor tridimensionale, precum și relațiile dintre acestea într-un context spațial. Deși este adesea percepută ca o disciplină abstractă, geometria în spațiu are o multitudine de aplicații practice în viața noastră de zi cu zi, influențând domenii precum arhitectura, ingineria, designul, navigația și chiar medicina. În acest articol, vom explora câteva dintre modurile în care geometria în spațiu este utilizată în viața reală.
Arhitectură și Design
Unul dintre cele mai evidente domenii în care geometria în spațiu este utilizată este arhitectura și designul. Arhitecții folosesc principiile geometrice pentru a proiecta și construi structuri impresionante și funcționale, cum ar fi clădiri, poduri și tuneluri. Geometria în spațiu este esențială pentru calcularea dimensiunilor, unghiurilor și proporțiilor în proiectarea acestor structuri, asigurându-se că acestea sunt stabile, sigure și estetice.
Inginerie și Construcții
În domeniul ingineriei și construcțiilor, geometria în spațiu joacă un rol crucial în proiectarea și construirea infrastructurii. Inginerii utilizează concepte geometrice pentru a calcula forțele și tensiunile care acționează asupra materialelor de construcție și pentru a proiecta structuri care să reziste la aceste presiuni. De la clădiri și autostrăzi până la structuri complexe, cum ar fi platformele offshore și stațiile spațiale, geometria în spațiu este prezentă în fiecare aspect al procesului de construcție.
Navigație și Cartografie
Geometria în spațiu este la baza sistemelor de navigație și cartografie moderne. GPS-ul (Sistemul de Poziționare Globală) utilizează principii geometrice pentru a determina poziția exactă a unui obiect în spațiu. Prin calcularea distanțelor și unghiurilor dintre receptorul GPS și sateliții de pe orbită, sistemul poate determina poziția cu o precizie extraordinară, facilitând navigația pe suprafața Pământului și în spațiu.
Medicină și Imagistică
În domeniul medicinii, geometria în spațiu este folosită în imagistica medicală pentru a obține imagini precise ale structurilor interne ale corpului uman. Tomografia computerizată și rezonanța magnetică utilizează algoritmi geometrici pentru a reconstrui imagini tridimensionale ale organelor și țesuturilor, ajutând medicii să diagnosticheze și să trateze diferite afecțiuni în mod eficient.
Concluzie
Geometria în spațiu nu este doar un concept abstract, ci și o unealtă practică și esențială în viața noastră de zi cu zi. De la proiectarea structurilor și navigarea în spațiu până la diagnosticarea bolilor și dezvoltarea tehnologiilor avansate, principiile geometrice stau la baza multor aspecte ale lumii moderne. Prin aplicarea acestor concepte în diferite domenii, continuăm să explorăm și să valorificăm potențialul lor pentru a îmbunătăți calitatea vieții noastre și pentru a avansa în cunoașterea umană. Geometria în spațiu este o unealtă puternică și versatilă, care ne ajută să înțelegem și să explorăm lumea din jurul nostru într-un mod precis și eficient.

