Înălțimi în corpurile geometrice studiate
Acest material despre înălțimi în corpurile geometrice studiate include următoarele noțiuni: înălțimea unei piramide, înălțimea unui con, înălțimea unei prisme, înălțimea unui cilindru, înălțimea unui trunchi de piramidă și înălțimea unui trunchi de con.

Înălțimea unei piramide
Înălțimea unei piramide reprezintă distanța de la vârful piramidei la planul bazei.
Într-o piramidă regulată înălțimea reprezintă distanța dintre vârful piramidei si centrul bazei.
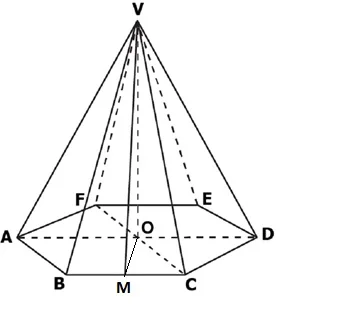
VO = Înălțime
Înălțimea unui con
Înălțimea unui con reprezintă distanța de vârful conului la planul bazei.
Într-un con circular drept, înălțimea reprezintă distanța dintre vârful conului si centrul bazei.
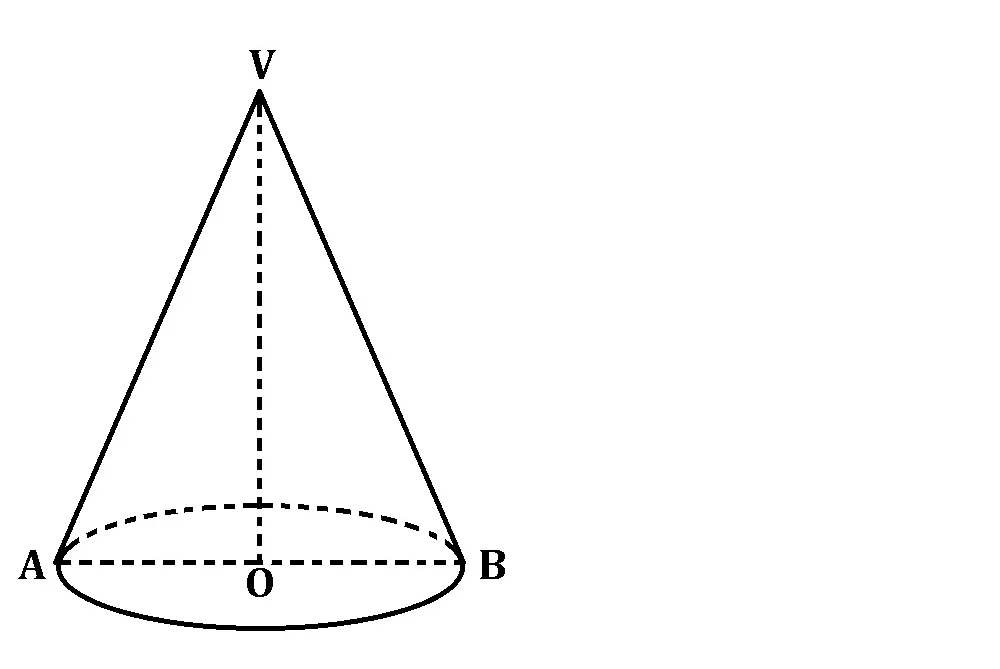
VO = Înălțime
Înălțimea unei prisme
Înălțimea unei prisme reprezintă distanța dintre planele bazelor.
În orice prismă dreaptă, muchiile laterale sunt înălțimi are prismei.
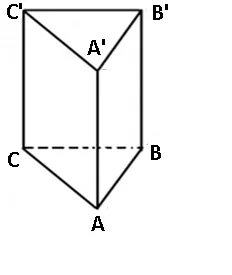
AA’, BB’, CC’ = Înălțimi
Înălțimea unui cilindru
Înălțimea unui cilindru reprezintă distanța dintre planele bazelor.
Oricare dintre generatoarele cilindrului circular drept, precum și distanța dintre centrele bazelor reprezintă înălțimi ale cilindrului.
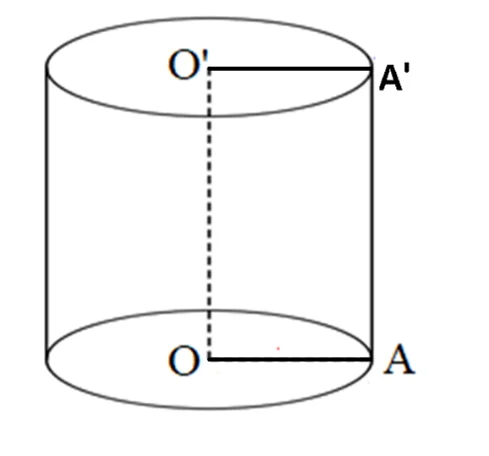
OO’, AA’ = Înălțimi
Înălțimea unui trunchi de piramidă
Înălțimea unui trunchi de piramidă reprezintă distanța dintre planele bazelor trunchiului de piramidă.
Într-un trunchi de piramidă regulată, distanța dintre centrele bazelor este o înălțime.
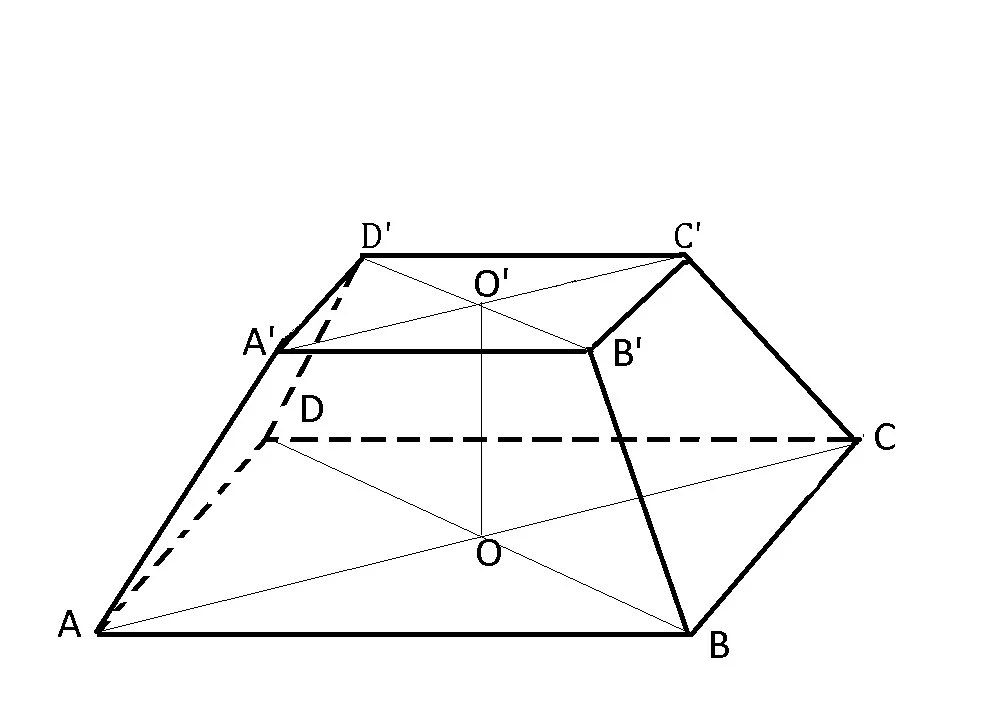
OO’=Înălțime
Înălțimea unui trunchi de con
Înălțimea unui trunchi de con reprezintă distanța dintre planele bazelor trunchiului de con.
Într-un trunchi de con circular drept, distanța dintre centrele bazelor este o înălțime.
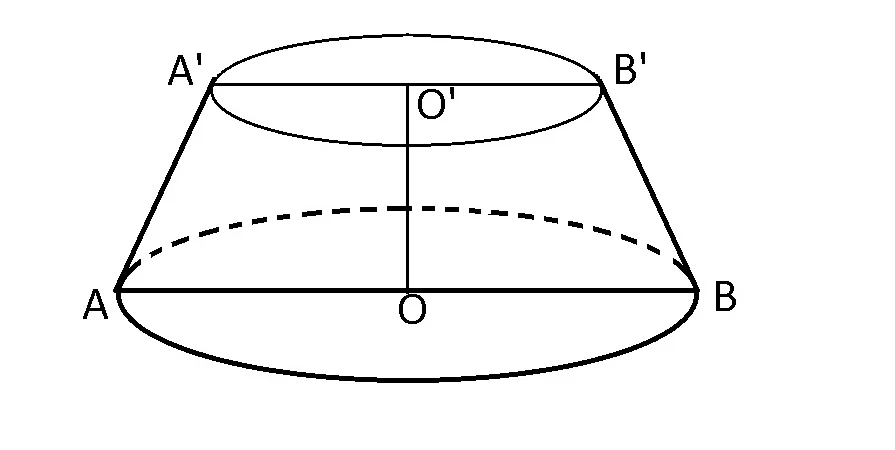
OO’=Înălțime
Utilizare Înălțimi în corpurile geometrice
Geometria este adesea privită ca un domeniu abstract și teoretic, dar conceptele sale au aplicații practice în numeroase aspecte ale vieții noastre. Unul dintre aceste concepte fundamentale este cel al înălțimilor în corpurile geometrice. Înălțimile sunt linii perpendiculare trasate dintr-un punct specific al unei figuri geometrice către latura opusă sau spre un alt punct de referință. Deși la început aceste concepte pot părea abstracte, ele sunt esențiale în rezolvarea problemelor de calcul și în înțelegerea structurilor complexe. În ceea ce urmează, vom explora câteva dintre modurile în care înălțimile sunt utilizate în viața reală.
- În domeniul arhitecturii și ingineriei, înălțimile sunt esențiale pentru proiectarea și construcția clădirilor și structurilor. De exemplu, înălțimile sunt utilizate pentru a calcula volumul și suprafața unei variate game de forme, de la piramide și conuri la cilindri și prismei. Aceste calcule sunt cruciale pentru a determina materialele necesare și costurile asociate cu construcția.
- De asemenea, înălțimile sunt folosite pentru a determina poziția și dimensiunea elementelor arhitecturale, precum coloanele, stâlpii și ferestrele. Ele sunt, de asemenea, utile în proiectarea și construcția de scări, punți și alte structuri înalte, unde trebuie să se țină cont de echilibrul și stabilitatea acestora.
- Înălțimile sunt esențiale în domeniul topografiei și cartografiei pentru a crea hărți precise ale terenului și reliefului. Utilizând tehnici precum fotogrametria și teledetecția, se pot măsura înălțimile diferitelor caracteristici geografice, cum ar fi munții, văile și râurile. Aceste informații sunt esențiale pentru planificarea urbană, dezvoltarea infrastructurii și gestionarea resurselor naturale.
- Înălțimile sunt adesea utilizate în designul grafic și multimedia pentru a crea imagini și modele tridimensionale realiste. Designerii folosesc înălțimile pentru a controla perspectiva și adâncimea unei scene sau a unui obiect, conferind astfel realism și profunzime imaginilor și animațiilor.
- De asemenea, în domeniul graficii computerizate și al jocurilor video, înălțimile sunt utilizate pentru a defini și manipula terenurile și obiectele 3D, oferind astfel o experiență interactivă mai captivantă pentru utilizatori.
Concluzie
Înălțimile în corpurile geometrice sunt concepte fundamentale care au o multitudine de aplicații practice în viața reală, de la arhitectură și inginerie la topografie și design grafic. Înțelegerea și aplicarea acestor concepte nu numai că facilitează rezolvarea problemelor tehnice și calcularea dimensiunilor, dar și inspiră creativitatea și inovația în diverse domenii. Prin urmare, este esențial să recunoaștem importanța și relevanța acestor concepte în lumea modernă și să le integrăm în practica noastră cotidiană.

