Proiecții ortogonale în spațiu
Acest material despre proiecții ortogonale în spațiu cuprinde următoarele noțiuni: proiecția unui punct pe un plan, proiecția unei drepte pe un plan, unghiul dintre o dreaptă și un plan, unghiul diedru și unghiul dintre două plane.

Proiecția unui punct pe un plan
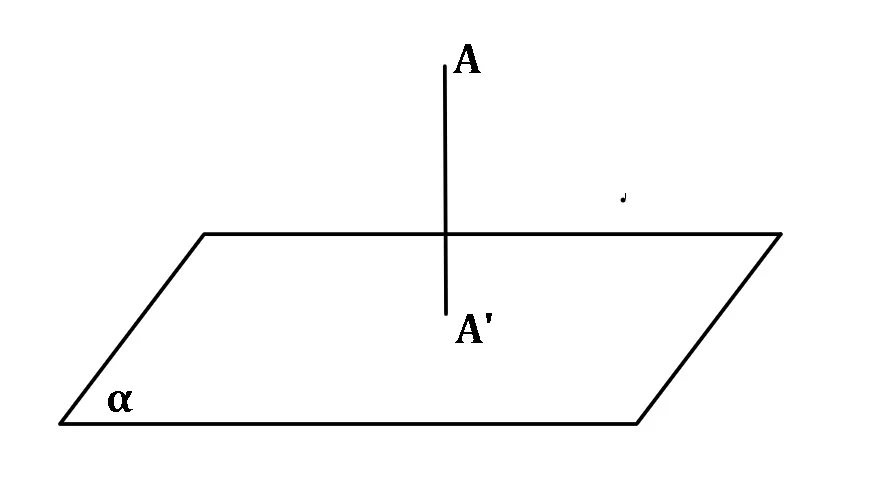
Proiecția unui punct A pe un plan α este punctul de intersecție al perpendicularei din A pe α cu planul α.
prαA = A’, unde AA’⊥ α, AA’∩α = {A’}, A∉α
Proiecția unei drepte pe un plan
Proiecția unei drepte pe un plan este:
- un punct, dacă dreapta este perpendiculară pe plan
- o dreaptă, dacă dreapta nu este perpendiculară pe plan
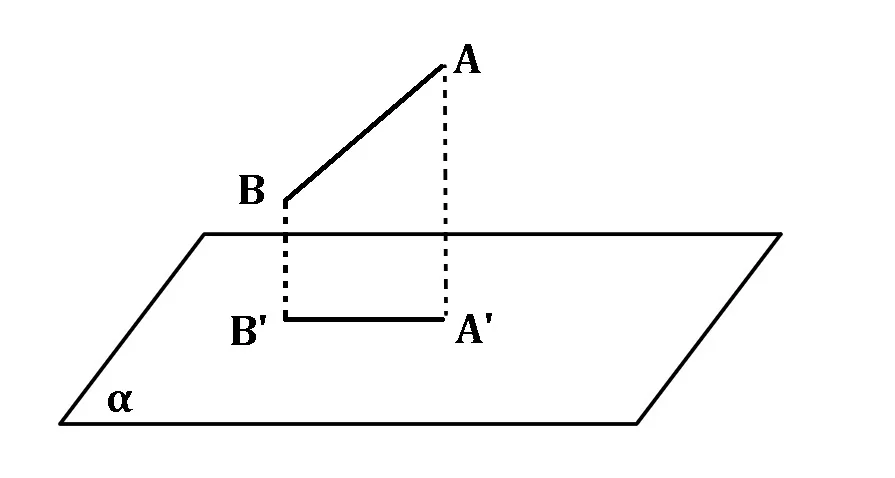
Proiecția segmentului AB pe planul α este un segment în acel plan, ale cărui capete reprezintă proiecțiile capetelor segmentului AB pe planul α.
prαA = A’, prαB = B’, A,B∉α => prαAB=A’B’
Unghiul dintre o dreaptă și un plan
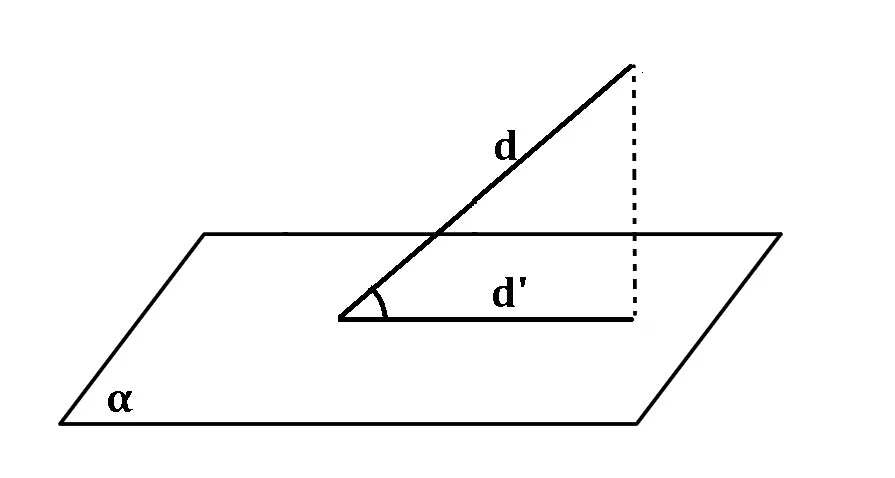
Unghiul dintre o dreaptă și un plan este unghiul format de acea dreaptă cu proiecția ei pe acel plan.
m∠(d,α) = m∠(d,d’) , unde d’ = prαd
Dacă o dreaptă este paralelă cu un plan, atunchi măsura unghiului dintre acea draptă și acel plan este de 0°.
Dacă o dreaptă este perpendiculară pe un plan, atunci măsura unghiului dintre acea dreaptă și acel plan este de 90°.
Unghiul diedru
Diedrul este firgura geometrică formată de două semiplane, mărginite de aceeași dreaptă.
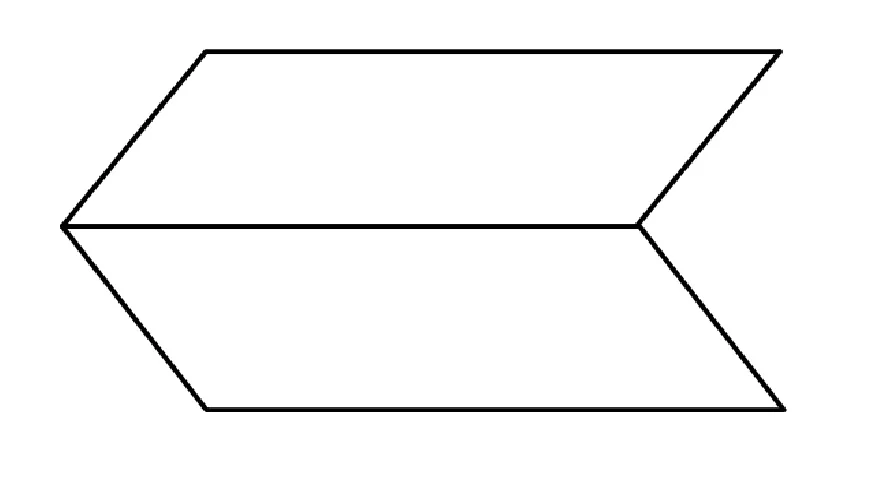
Unghiul plan al unghiului diedru este unghiul determinat de intersecția diedrului cu un plan perpendicular pe muchia sa.
Măsura unui unghi diedru este măsura unghiului plan corespunzător unghiului diedru.
Măsura unghiului dintre două plane este egală cu măsura unui diedru ascuțit sau drept format de acestea.
Măsura unghiului dintre două plane este egală cu măsura unghiului dintre o dreaptă din primul plan și o dreaptă din cel de-al doilea plan, ambele perpendiculare pe dreapta de intersecție a celor două plane.
m∠(α, β) = m∠(a, b), unde a∈α, b∈β, a⊥d, b⊥d, iar {d}=α∩β.

Utilizare Proiecții ortogonale în spațiu
Proiecțiile ortogonale în spațiu reprezintă un concept fundamental în geometria descriptivă și inginerie, având o gamă largă de aplicații practice în numeroase domenii. Aceste proiecții oferă o metodă eficientă de a reprezenta obiecte tridimensionale pe planuri bidimensionale, facilitând astfel comunicarea și înțelegerea detaliilor geometrice complexe. În acest articol, vom explora câteva dintre utilizările proiecțiilor ortogonale în viața reală.
- În domeniul designului industrial și ingineriei, proiecțiile ortogonale sunt utilizate pentru a realiza desene tehnice detaliate ale componentelor și asamblajelor mecanice. Aceste desene oferă informații precise despre dimensiuni, forme și poziții, esențiale în procesul de fabricație și asamblare a produselor. Prin intermediul proiecțiilor ortogonale, inginerii pot comunica clar și eficient cerințele de proiectare și specificațiile tehnice către echipele de producție, facilitând astfel dezvoltarea și fabricarea produselor de înaltă calitate.
- În domeniul arhitecturii și designului interior, proiecțiile ortogonale sunt utilizate pentru a crea planuri și elevații ale clădirilor și spațiilor interioare. Aceste proiecții permit arhitecților și designerilor să vizualizeze și să analizeze în detaliu proporțiile, distribuția spațiilor și aspectul estetic al proiectelor lor.
- Prin intermediul proiecțiilor ortogonale, se pot identifica și soluționa potențialele probleme de proiectare în stadiile incipiente ale procesului de design, contribuind astfel la optimizarea funcționalității și esteticii spațiilor construite.
- În domeniul geodeziei și cartografiei, proiecțiile ortogonale sunt utilizate pentru a reprezenta suprafețele sferice ale Pământului pe planuri plane, ceea ce facilitează crearea și interpretarea hărților geografice precise și detaliate. Prin intermediul proiecțiilor ortogonale, se pot măsura și analiza diverse caracteristici geografice, cum ar fi elevația terenului, distribuția vegetației și cursurile de apă, contribuind astfel la planificarea urbană, gestionarea resurselor naturale și navigația terestră și aeriană.
Concluzie
Proiecțiile ortogonale în spațiu sunt instrumente indispensabile într-o varietate de domenii, de la design industrial și inginerie la arhitectură și cartografie. Aceste proiecții permit reprezentarea clară și precisă a obiectelor tridimensionale pe planuri bidimensionale, facilitând comunicarea și înțelegerea detaliilor geometrice complexe în diverse contexte. Prin urmare, este esențial să recunoaștem importanța și relevanța acestor proiecții în lumea modernă și să le utilizăm în mod eficient în practica noastră cotidiană.

