Teorema celor trei perpendiculare
Acest material despre teorema celor trei perpendiculare cuprinde următoarele noțiuni: teorema celor trei perpendiculare, prima reciprocă a teoremei celor trei perpendiculare, a doua reciprocă a teoremei celor trei perpendiculare.

Teorema celor trei perpendiculare
Fie un plan α, un punct M∉α și o dreaptă d ⊂ α.
Dacă MA ⊥ α, A ∈ α și AB ⊥ d, B ∈ d, atunci MB ⊥ d.
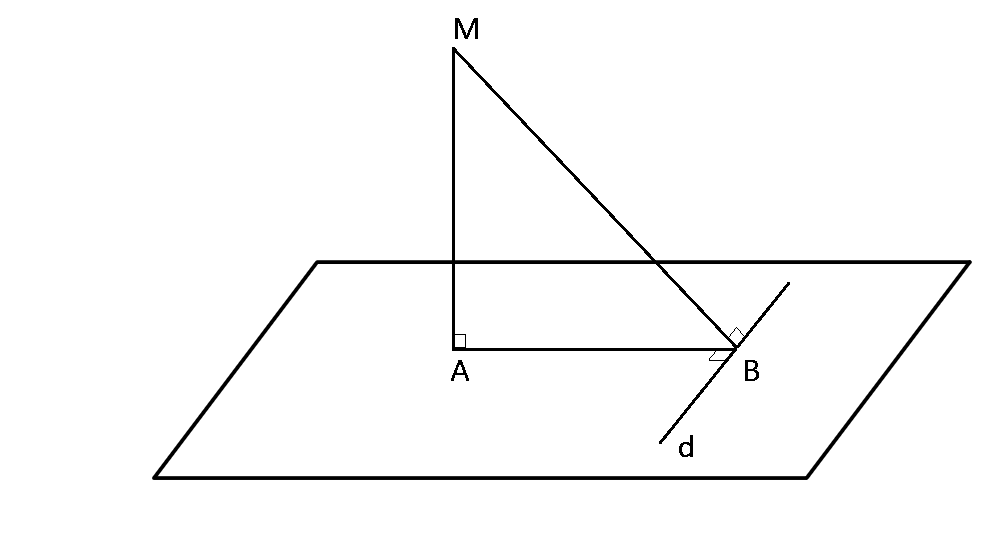
Demonstrație:
MA ⊥ α, dar d ⊂ α, așadar: MA ⊥ d sau d ⊥MA. (Dacă o dreaptă este perpendiculară pe un plan, atunci acea dreaptă este perpendiculară pe orice dreaptă din acel plan).
Dar AB ⊥ d sau d ⊥ AB.
MA ∩ AB = {A}
MA, AB ⊂ (MAB)
Așadar avem d ⊥ (MAB). (Dacă o dreaptă este perpendiculară pe două drepte concurente incluse într-un plan, atunci acea dreaptă este perpendiculară pe acel plan).
MB ⊂ (MAB)
Deci d ⊥ MB sau MB ⊥ d.
Pornind de la teorema celor trei perpendiculare, pot fi formulate două reciproce, ambele adevărate. Cele două teoreme reciproce sunt prezentate în cele ce urmează.
Prima reciprocă a teoremei celor trei perpendiculare
Se consideră un plan α, o dreaptă d ⊂ α și un punct M ∉ α.
Dacă MA ⊥ α, A ∈ α, punctul B ∈ d astfel încât MB ⊥ d, atunci AB ⊥ d.
Cea de-a doua reciprocă a teoremei celor trei perpendiculare
Se consideră un plan α, o dreaptă d ⊂ α, un punct M ∉ α și un punct A ∈ α.
Dacă AB ⊥ d, B ∈ d, MB ⊥ d și MA ⊥ A′B, atunci MA ⊥ α.
Utilizate Teorema celor trei perpendiculare
Teorema celor trei perpendiculare este un concept geometric fundamental care afirmă că în orice triunghi, trei perpendiculare duse de la vârfurile triunghiului la laturile opuse se intersectează într-un singur punct, numit ortocentrul. Această teoremă este esențială în geometrie și are o serie de aplicații practice în diverse domenii. În acest articol, vom explora câteva dintre utilizările teoremei celor trei perpendiculare în viața reală.
1. Cartografie și Topografie
În domeniul cartografiei și topografiei, teorema celor trei perpendiculare este utilizată pentru a determina înălțimile punctelor de pe teren în raport cu nivelul de referință. Prin măsurarea unghiurilor și lungimilor dintriunghiuri, topografii pot calcula și reprezenta relieful terenului în mod precis pe hărți și planuri.
Această informație este crucială în planificarea urbană, construcția de infrastructură și gestionarea resurselor naturale, permitând autorităților și organizațiilor să ia decizii informate în ceea ce privește dezvoltarea și utilizarea terenurilor.
2. Design Interior și Arhitectură
În domeniul designului interior și al arhitecturii, teorema celor trei perpendiculare este utilizată pentru a determina poziționarea și dimensiunile elementelor spațiilor interioare și exterioare. Designerii folosesc această teoremă pentru a crea spații echilibrate și armonioase, luând în considerare intersecțiile și unghiurile formate de pereți, ferestre și alte elemente arhitecturale.
Prin aplicarea teoremei celor trei perpendiculare, se poate obține un design funcțional și estetic, care să îndeplinească cerințele și preferințele clienților în ceea ce privește confortul și utilitatea spațiilor construite.
3. Navigație și Construcții Navale
În domeniul navigației și al construcțiilor navale, teorema celor trei perpendiculare este utilizată pentru a determina punctele de echilibru și stabilitate ale navelor și structurilor maritime. Inginerii navali folosesc această teoremă pentru a proiecta și construi nave și platforme offshore care să reziste la forțele naturale, cum ar fi valurile și vânturile puternice.
Prin aplicarea teoremei celor trei perpendiculare, se poate asigura că navelor și structurilor maritime le sunt distribuite corect greutatea și centrul de masă, minimizând riscul de efracție sau accidente în timpul navigației și utilizării acestora pe mare.
Concluzie
Teorema celor trei perpendiculare este un concept geometric esențial cu numeroase aplicații practice în diverse domenii, cum ar fi cartografia, designul interior, arhitectura, navigația și construcțiile navale. Această teoremă oferă o modalitate simplă și eficientă de a calcula și de a reprezenta relațiile geometrice între puncte, linii și planuri, facilitând astfel proiectarea și construcția structurilor și obiectelor în lumea reală. Prin urmare, este important să recunoaștem importanța și relevanța teoremei celor trei perpendiculare și să o utilizăm în mod corespunzător în practica noastră cotidiană.

