Patrulaterul convex. Paralelogramul

Acest material despre patrulatere cuprinde următoarele noțiuni: patrulaterul convex și paralelogramul.

Patrulaterul convex

Patrulaterul este un poligon cu patru laturi.

Patrulaterul convex are toate unghiurile interioare cu măsurile mai mici de 180°.

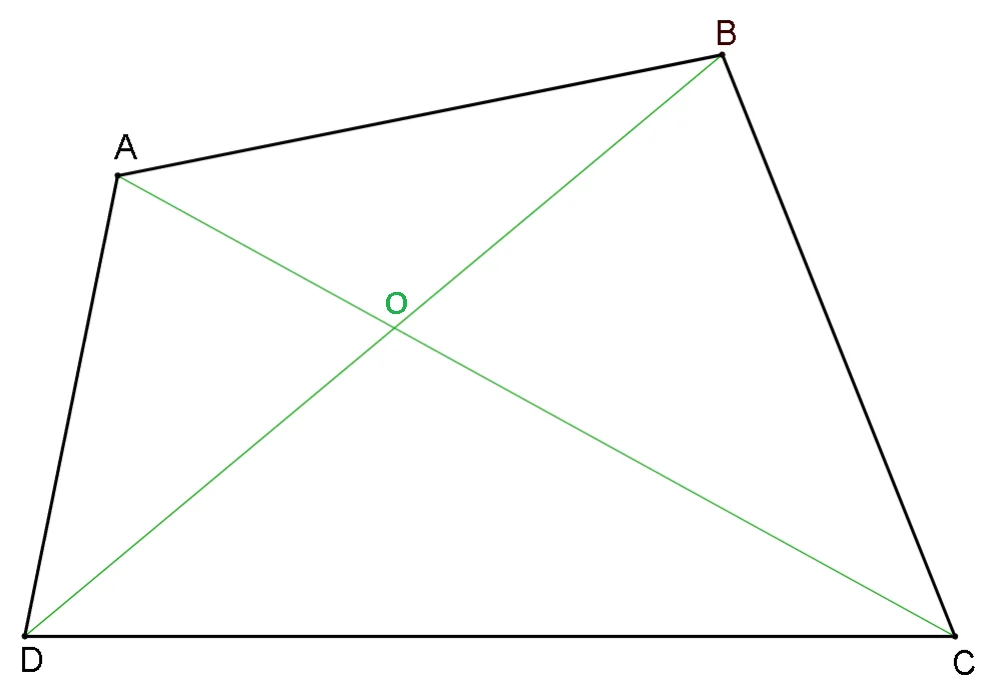
ABCD-patrulater convex:

A,B,C,D = vârfuri
AB, BC, CD, DA = laturi
AC, BD = diagonale
∢A (∢DAB), ∢B (∢ABC), ∢C(∢BCD), ∢D(∢CDA) = unghiurile patrulaterului.

Suma măsurilor unghiurilor unui patrulater convex este 360°:

m∢A+m∢B+m∢C+m∢D = 360°

Perimetrul unui patrulater convex este suma celor patru laturi:

P_ABCD = AB+BC+CD+DA

Paralelogramul

Paralelogramul este patrulaterul convex cu laturile opuse paralele două câte două.

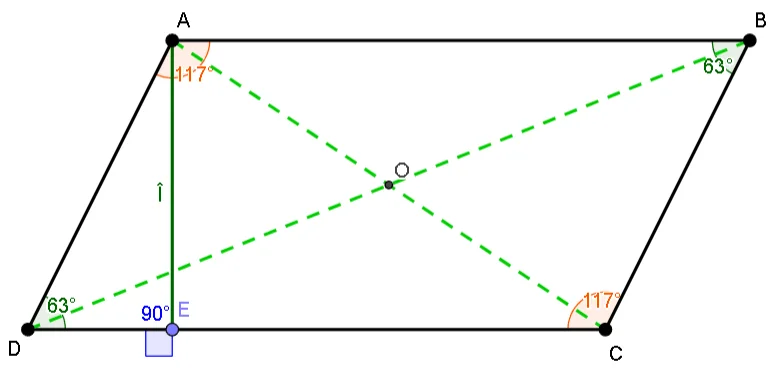
ABCD – patrulater convex, AB||CD și BC||AD $\implies$ ABCD paralelogram

Proprietățile paralelogramului:

Laturile opuse sunt congruente: AB=CD și BC=AD;

Unghiurile opuse sunt congruente: m∢A=m∢C și m∢B=m∢D;

Unghiurile alăturate sunt suplementare: m∢A+m∢B= m∢B+m∢C= m∢C+m∢D= m∢D+m∢A = 180°

Diagonalele se înjumătățesc: AC ∩ BD = {O} AO=OC= 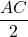$\dfrac{AC}{2}$ și BO=OD=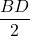 $\dfrac{BD}{2}$

Perimetrul paralelogramului: P_ABCD = AB+BC+CD+DA;

Aria paralelogramului: A_ABCD= b·h = CD·AE, unde AE⊥CD,E∈CD sau A_ABCD=A_ΔABC+A_ΔADC(sau A_ΔABD+A_ΔCBD).

Cum arătăm că un patrulater este paralelogram?

arătăm că are laturile opuse paralele două câte două: AB||CD și BC||AD $\implies$ ABCD paralelogram

arătăm că are laturile opuse congruente două câte două: AB=CD și BC=AD $\implies$ ABCD paralelogram

arătăm ca are o pereche de laturi opuse paralele și congurente. Exemplu: AB=CD și AB||CD $\implies$ ABCD paralelogram

arătăm că are unghiurile opuse congruente două câte două: m∢A=m∢C și m∢B=m∢D $\implies$ ABCD paralelogram

arătăm că diagonalele se înjumătățesc: AC∩BD={O}, O este mijlocul lui AC și O este mijlocul lui BD $\implies$ ABCD paralelogram

Utilizare

Paralelogramul este un concept important în geometrie și se referă la o figura plană formată din patru laturi paralele și două perechi de laturi congruente. Acest concept este utilizat în mai multe domenii și aplicații, precum:

Geometrie – Paralelogramul este studiat în detaliu în geometrie și este esențial pentru înțelegerea conceptelor legate de forme și dimensiuni.
Inginerie – Paralelogramul este utilizat în inginerie pentru a modela structuri sau obiecte, cum ar fi clădirile, precum și pentru a calcula proprietățile fizice ale acestora.
Grafică computerizată – Paralelogramul este utilizat în grafica computerizată pentru a crea obiecte tridimensionale sau pentru a modela imagini în jocuri video sau animații.
Arhitectură – Paralelogramul este utilizat în arhitectură pentru a modela formele clădirilor sau pentru a proiecta planurile acestora.

În concluzie, paralelogramul este un concept important în mai multe domenii, fiind utilizat în geometrie, inginerie, grafica computerizată și arhitectură, și este esențial pentru înțelegerea și aplicarea acestor domenii.

Dacă îți place platforma noastră, te invit și pe pagina noastră de Facebook și Youtube

Meniu